Advertisements
Advertisements
Question
AB और AC त्रिज्या r वाले एक वृत्त की दो जीवाएँ इस प्रकार हैं कि AB = 2AC है। यदि p और q क्रमश : केंद्र से AB और AC की दूरियाँ हैं, तो सिद्ध कीजिए कि 4q2 = p2 + 3r2 है।
Solution
दिया गया है - r त्रिज्या के एक वृत्त में दो जीवाएँ AB और AC इस प्रकार हैं कि AB = 2AC है। साथ ही, केंद्र से AB और AC की दूरियाँ क्रमश : p और q हैं।
सिद्ध करना है - 4q2 = p2 + 3r2
उपपत्ति - माना AC = a, तब AB = 2a
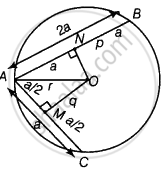
केंद्र O से जीवा AC और AB पर क्रमश : M और N पर लंब खींचा जाता है।
∴ `AM = MC = a/2`
AN = NB = a
ΔOAM में, AO2 = AM2 + MO2 ...[पाइथागोरस प्रमेय द्वारा]
⇒ `AO^2 = (a/2)^2 + q^2` ...(i)
ΔOAN में, पाइथागोरस प्रमेय का प्रयोग करें,
AO2 = (AN)2 + (NO)2
⇒ AO2 = (a)2 + p2 ...(ii)
समीकरण (i) और (ii) से,
`(a/2)^2 + q^2 = a^2 + p^2`
⇒ `a^2/4 + q^2 = a^2 + p^2`
⇒ a2 + 4q2 = 4a2 + 4p2 ...[दोनों पक्षों को 4 से गुणा करने पर]
⇒ 4q2 = 3a2 + 4p2
⇒ 4q2 = p2 + 3(a2 + p2)
⇒ 4q2 = p2 + 3r2 ...[समकोण ΔOAN में, r2 = a2 + p2]
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
आकृति में, केंद्र O वाले एक वृत्त पर तीन बिन्दु A, B और C इस प्रकार हैं कि ∠BOC = 30० तथा ∠AOB = 60० है। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिंदु है, तो ∠ADC ज्ञात कीजिए।

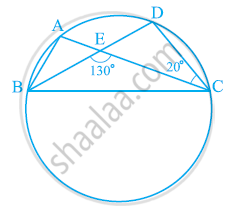
आकृति में, एक वृत्त पर A, B, C और D चार बिंदु हैं। AC और BD एक बिंदु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠BEC = 130° तथा ∠ECD = 20° है। ∠BAC ज्ञात कीजिए।
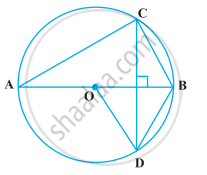
निम्नलिखित आकृति में, यदि AOB एक व्यास है और ∠ADC = 120° है, तो ∠CAB = 30° है।
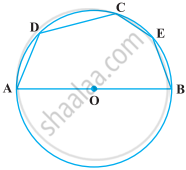
यदि एक वृत्त के चाप AXB और CYD सर्वांगसम हैं तो AB और CD का अनुपात ज्ञात कीजिए।
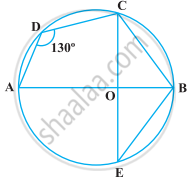
निम्नलिखित आकृति में, ∠ADC = 130° और जीवा BC = जीवा BE है। ∠CBE ज्ञात कीजिए।
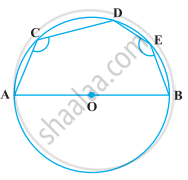
निम्नलिखित आकृति में, AOB वृत्त का व्यास है तथा C, D और E अर्धवृत्त पर स्थित कोई तीन बिंदु हैं। ∠ACD + ∠BED का मान ज्ञात कीजिए।
निम्नलिखित आकृति में, ∠OAB = 30° और ∠OCB = 57° है। ∠BOC और ∠AOC ज्ञात कीजिए।

निम्नलिखित आकृति में, AB और CD एक वृत्त की दो जीवाएँ हैं, जो E पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि AEC = `1/2` (चाप CXA द्वारा केंद्र पर अंतरित कोण + चाप DYB द्वारा केंद्र पर अंतरित कोण) है।
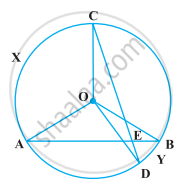
निम्नलिखित आकृति में, O वृत्त का केंद्र है और ∠BCO = 30° है। x और y ज्ञात कीजिए।
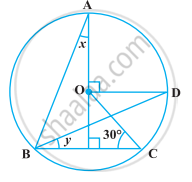
निम्नलिखित आकृति में, O वृत्त का केंद्र है, BD = OD और CD ⊥ AB है। ∠CAB ज्ञात कीजिए।