Advertisements
Advertisements
Question
एक वृत्त की दो बराबर AB और CD जीवाएँ बढ़ाने पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि PB = PD है।
Solution
दिया गया है - एक वृत्त की दो समान जीवाएँ AB और CD एक बिंदु P पर प्रतिच्छेद करती हैं।
सिद्ध करना है - PB = PD
रचना - OP को मिलाइए, OL ⊥ AB और OM ⊥ CD खींचिए।
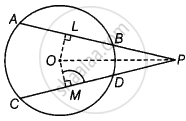
प्रमाण - हमारे पास है, AB = CD
⇒ OL = OM ...[समान जीवाएँ केंद्र से समदूरस्थ होती हैं।]
ΔOLP तथा ΔOMP में,
OL = OM ...[ऊपर सिद्ध]
∠OLP = ∠OMP ...[प्रत्येक 90°]
और OP = OP ...[उभयनिष्ठ पक्ष]
∴ ΔOLP ≅ ΔOMP ...[RHS सर्वांगसमता नियम द्वारा]
⇒ LP = MP [CPCT द्वारा] ...(i)
अब, AB = CD
⇒ `1/2 (AB) = 1/2 (CD)` ...[दोनों पक्षों को 2 से विभाजित करने पर]
⇒ BL = DM ...(ii) [केंद्र से जीवा को समद्विभाजित करने के लिए खींचा गया लंब अर्थात AL = LB और CM = MD]
समीकरण (ii) और समीकरण (i) को घटाने पर, हम पाते हैं।
LP – BL = MP – DM
⇒ PB = PD
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
आकृति में, केंद्र O वाले एक वृत्त पर तीन बिन्दु A, B और C इस प्रकार हैं कि ∠BOC = 30० तथा ∠AOB = 60० है। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिंदु है, तो ∠ADC ज्ञात कीजिए।

निम्नलिखित आकृति में, यदि AOB एक व्यास है और ∠ADC = 120° है, तो ∠CAB = 30° है।
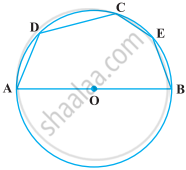
यदि एक वृत्त के चाप AXB और CYD सर्वांगसम हैं तो AB और CD का अनुपात ज्ञात कीजिए।
AB और AC एक वृत्त की दो बराबर जीवाएँ हैं। सिद्ध कीजिए कि ∠BAC का समद्विभाजक वृत्त के केंद्र से होकर जाता है।
यदि वृत्त की दो जीवाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड वृत्त के केंद्र से होकर जाता है, तो सिद्ध कीजिए कि दोनों जीवाएँ समांतर है।
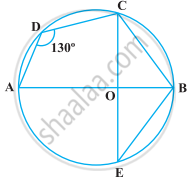
निम्नलिखित आकृति में, ∠ADC = 130° और जीवा BC = जीवा BE है। ∠CBE ज्ञात कीजिए।
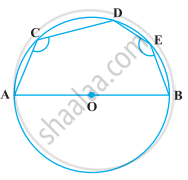
निम्नलिखित आकृति में, AOB वृत्त का व्यास है तथा C, D और E अर्धवृत्त पर स्थित कोई तीन बिंदु हैं। ∠ACD + ∠BED का मान ज्ञात कीजिए।
सिद्ध कीजिए कि एक त्रिभुज के किसी कोण का समद्विभाजक और उसकी सम्मुख भुजा का लंब समद्विभाजक, यदि प्रतिच्छेद करते हैं तो, उस त्रिभुज के परिवृत्त पर प्रतिच्छेद करते हैं।
यदि ABC किसी वृत्त के अंतर्गत एक समबाहु त्रिभुज है तथा P लघु चाप BC पर स्थित कोई बिंदु है, जो B या C के संपाती नहीं है, तो सिद्ध कीजिए कि PA कोण BPC का समद्विभाजक हैं।
AB और AC त्रिज्या r वाले एक वृत्त की दो जीवाएँ इस प्रकार हैं कि AB = 2AC है। यदि p और q क्रमश : केंद्र से AB और AC की दूरियाँ हैं, तो सिद्ध कीजिए कि 4q2 = p2 + 3r2 है।
