Advertisements
Advertisements
Question
सिद्ध कीजिए कि एक त्रिभुज के किसी कोण का समद्विभाजक और उसकी सम्मुख भुजा का लंब समद्विभाजक, यदि प्रतिच्छेद करते हैं तो, उस त्रिभुज के परिवृत्त पर प्रतिच्छेद करते हैं।
Solution
दिया गया है - ΔABC एक वृत्त के अंतर्गत है। ∠A का समद्विभाजक और BC का लंब समद्विभाजक बिंदु Q पर प्रतिच्छेद करता है।
सिद्ध करना है - A, B, Q और C संचक्रीय हैं।
रचना - BQ और QC को मिलाइए।
उपपत्ति - हमने माना है कि, Q वृत्त के बाहर स्थित है।
∆BMQ और ∆CMQ में,
BM = CM ...[QM BC का लंबवत द्विभाजक है।]
∠BMQ = ∠CMQ ...[प्रत्येक 90°]
MQ = MQ ...[सामान्य पक्ष]
∴ ΔBMQ ≅ ΔCMQ ...[SAS सर्वांगसमता नियम द्वारा]
∴ BQ = CQ [CPCT द्वारा] ...(i)
साथ ही, ∠BAQ = ∠CAQ [दिया गया है।] ...(ii)
समीकरण (i) और (ii) से,
हम कह सकते हैं कि Q वृत्त पर स्थित है। ...[वृत्त की समान जीवाएँ परिधि पर समान कोण बनाती हैं।]
अतः, A, B, Q और C अचक्रीय हैं।
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
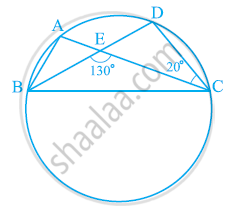
आकृति में, एक वृत्त पर A, B, C और D चार बिंदु हैं। AC और BD एक बिंदु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠BEC = 130° तथा ∠ECD = 20° है। ∠BAC ज्ञात कीजिए।
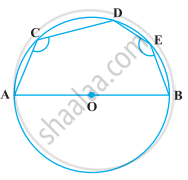
यदि एक वृत्त के चाप AXB और CYD सर्वांगसम हैं तो AB और CD का अनुपात ज्ञात कीजिए।
AB और AC एक वृत्त की दो बराबर जीवाएँ हैं। सिद्ध कीजिए कि ∠BAC का समद्विभाजक वृत्त के केंद्र से होकर जाता है।
यदि वृत्त की दो जीवाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड वृत्त के केंद्र से होकर जाता है, तो सिद्ध कीजिए कि दोनों जीवाएँ समांतर है।
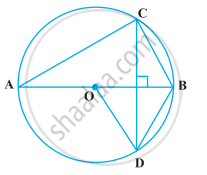
निम्नलिखित आकृति में, AOB वृत्त का व्यास है तथा C, D और E अर्धवृत्त पर स्थित कोई तीन बिंदु हैं। ∠ACD + ∠BED का मान ज्ञात कीजिए।
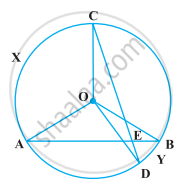
यदि ABC किसी वृत्त के अंतर्गत एक समबाहु त्रिभुज है तथा P लघु चाप BC पर स्थित कोई बिंदु है, जो B या C के संपाती नहीं है, तो सिद्ध कीजिए कि PA कोण BPC का समद्विभाजक हैं।
निम्नलिखित आकृति में, AB और CD एक वृत्त की दो जीवाएँ हैं, जो E पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि AEC = `1/2` (चाप CXA द्वारा केंद्र पर अंतरित कोण + चाप DYB द्वारा केंद्र पर अंतरित कोण) है।
एक वृत्त की दो बराबर AB और CD जीवाएँ बढ़ाने पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि PB = PD है।
AB और AC त्रिज्या r वाले एक वृत्त की दो जीवाएँ इस प्रकार हैं कि AB = 2AC है। यदि p और q क्रमश : केंद्र से AB और AC की दूरियाँ हैं, तो सिद्ध कीजिए कि 4q2 = p2 + 3r2 है।
निम्नलिखित आकृति में, O वृत्त का केंद्र है, BD = OD और CD ⊥ AB है। ∠CAB ज्ञात कीजिए।