Advertisements
Advertisements
Question
निम्नलिखित आकृति में, यदि AOB एक व्यास है और ∠ADC = 120° है, तो ∠CAB = 30° है।
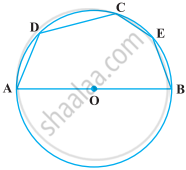
Options
सत्य
असत्य
Solution
यह कथन सत्य है।
स्पष्टीकरण -
माना AOB वृत्त का व्यास है।
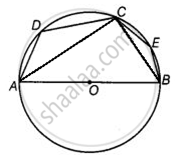
दिया गया है - ∠ADC = 120°
सबसे पहले, CB से जुड़ें।
फिर, हमारे पास एक चक्रीय चतुर्भुज ABCD है।
चूँकि एक चक्रीय चतुर्भुज के सम्मुख कोणों का योग 180° होता है, इसलिए
∠ADC + ∠ABC = 180°
⇒ 120° + ∠ABC = 180°
⇒ ∠ABC = 180° – 120°
⇒ ∠ABC = 60°
अब AC से जुड़ें।
साथ ही, व्यास वृत्त के साथ एक समकोण बनाता है,
∴ ∆ABC में, ∠ACB = 90° है।
अब, त्रिभुज के कोण गुण के अनुसार त्रिभुज के सभी कोणों का योग 180° होता है।
∴ ∠CAB + ∠ABC + ∠ACB = 180°
⇒ ∠CAB + 60° + 90° = 180°
⇒ ∠CAB = 180° – 90° – 60°
⇒ ∠CAB = 30°
APPEARS IN
RELATED QUESTIONS
आकृति में, ∠ABC = 69° और ∠ACB = 31° हो, तो ∠BDC ज्ञात कीजिए।
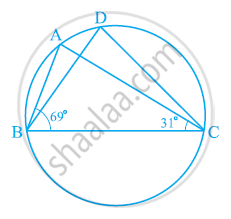
आकृति में, एक वृत्त पर A, B, C और D चार बिंदु हैं। AC और BD एक बिंदु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠BEC = 130° तथा ∠ECD = 20° है। ∠BAC ज्ञात कीजिए।
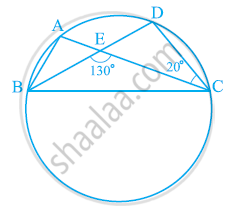
AB और AC एक वृत्त की दो बराबर जीवाएँ हैं। सिद्ध कीजिए कि ∠BAC का समद्विभाजक वृत्त के केंद्र से होकर जाता है।
यदि वृत्त की दो जीवाओं के मध्य-बिंदुओं को मिलाने वाला रेखाखंड वृत्त के केंद्र से होकर जाता है, तो सिद्ध कीजिए कि दोनों जीवाएँ समांतर है।
किसी वृत्त की एक जीवा उसकी त्रिज्या के बराबर है। इस जीवा द्वारा दीर्घ वृत्तखंड में किसी बिंदु पर अंतरित कोण ज्ञात कीजिए।
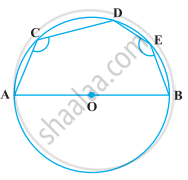
निम्नलिखित आकृति में, AOB वृत्त का व्यास है तथा C, D और E अर्धवृत्त पर स्थित कोई तीन बिंदु हैं। ∠ACD + ∠BED का मान ज्ञात कीजिए।
निम्नलिखित आकृति में, ∠OAB = 30° और ∠OCB = 57° है। ∠BOC और ∠AOC ज्ञात कीजिए।

यदि ABC किसी वृत्त के अंतर्गत एक समबाहु त्रिभुज है तथा P लघु चाप BC पर स्थित कोई बिंदु है, जो B या C के संपाती नहीं है, तो सिद्ध कीजिए कि PA कोण BPC का समद्विभाजक हैं।
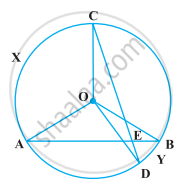
निम्नलिखित आकृति में, AB और CD एक वृत्त की दो जीवाएँ हैं, जो E पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि AEC = `1/2` (चाप CXA द्वारा केंद्र पर अंतरित कोण + चाप DYB द्वारा केंद्र पर अंतरित कोण) है।
AB और AC त्रिज्या r वाले एक वृत्त की दो जीवाएँ इस प्रकार हैं कि AB = 2AC है। यदि p और q क्रमश : केंद्र से AB और AC की दूरियाँ हैं, तो सिद्ध कीजिए कि 4q2 = p2 + 3r2 है।
