Question

ABC is a triangle whose vertices are A(3, 4), B(−2, −1) and C(5, 3). If G is the centroid and BDCG is a parallelogram then find the coordinates of the vertex D.

Answer 1

The vertices of a triangle are A(3, 4), B(−2, −1) and C(5, 3)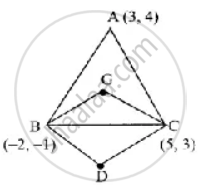

Centroid of a triangle (G) = `((x_1 + x_2 + x_3)/3, (y_1 + y_2 + y_3)/3)`

= `((3 - 2 + 5)/3, (4 - 1 + 3)/3)`

= `(6/3, 6/3)`

= (2, 2)

The point G is (2, 2)

Let the vertices D be (a, b)

Since BDCG is a parallelogram

Mid-point of BC = Mid-point of DG

`((-2 + 5)/2, (-1 + 3)/2) = ((2 + "a")/2, (2 + "b")/2)`

`(3/2, 1) = ((2 + "a")/2, (2 + "b")/2)`

`(2 + "a")/2 = 3/2`

4 + 2a = 6

2a = 6 – 4

2a = 2

a = 1

and 

`(2 + "b")/2` = 1

2 + b = 2

b = 2 – 2 = 0

The vertices D is (1, 0).