Advertisements
Advertisements
Question

Solution
□ABCD हा समांतरभुज चौकोन आहे. ...[पक्ष]
∴ बाजू AB || बाजू CD ...[समांतरभुज चौकोनाच्या संमुख बाजू]
∴ बाजू AB || बाजू CP ...[C - P - D]
व BP ही त्यांची छेदिका आहे.
∴ ∠CPB ≅ ∠ABP ...[व्युत्क्रम कोन]
∴ ∠CPX ≅ ∠ABX ...(i)[P - X - B]
ΔPXC व ΔBXA मध्ये,
∠PXC ≅ ∠BXA ...[परस्पर विरुद्ध कोन]
∠CPX ≅ ∠ABX ...[(i) वरून]
∴ ΔPXC ∼ ΔBXA ...[कोको कसोटीनुसार]
∴ `(CX)/(AX) = (XP)/(XB) = (AB)/(CP)` ...(ii)[समरूप त्रिकोणांच्या संगत बाजू]
लक्षात घ्या,
रेख AB ≅ रेख CD ...(iii) [∵ □ ABCD हा समांतरभुज चौकोन आहे.]
रेख CP = `1/2` रेख CD ...(iv) [P हा बाजू CD चा मध्यबिंदू आहे.]
∴ रेख CP = `1/2` रेख AB ...(v) [(iii) व (iv)]
∴ `(CX)/(AX) = (XP)/(XB) = (AP)/(CB) = 2/1` ...[(ii) व (v) वरून]
∴ `(CX)/(AX) = 2/1`
∴ `(CX + AX)/(AX) = (2 + 1)/2` ...[योग क्रियेने]
∴ `(AC)/(AX) = 3/2`
∴ 3AX = 2AC हे सिद्ध होते.
APPEARS IN
RELATED QUESTIONS
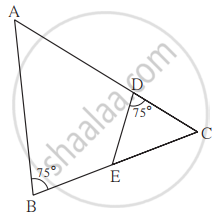
आकृती मध्ये ∠ABC = 75°, ∠EDC =75° तर कोणते दोन त्रिकोण कोणत्या कसोटीनुसार समरूप आहेत? त्यांची समरूपता योग्य एकास एक संगतीत लिहा.
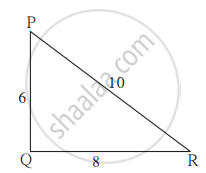
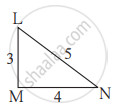
आकृती मधील त्रिकोण समरूप आहेत का? असतील तर कोणत्या कसोटीनुसार?
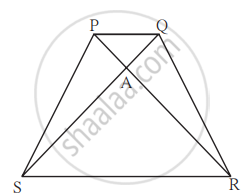
आकृतीत समलंब चौकोन PQRS मध्ये, बाजू PQ || बाजू SR, AR = 5AP, AS = 5AQ तर सिद्ध करा, SR = 5PQ.
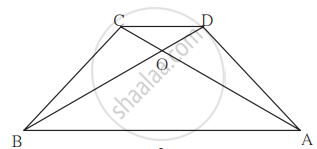
समलंब चौकोन ABCD मध्ये, बाजू AB || बाजू DC कर्ण AC व कर्ण BD हे परस्परांना O बिंदूत छेदतात. AB = 20, DC = 6, OB = 15 तर OD काढा.
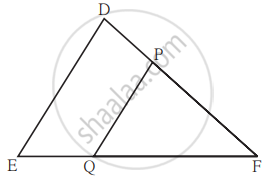
आकृती मध्ये रेख PQ || रेख DE, A (Δ PQF) = 20 एकक, जर PF = 2 DP आहे, तर A(`square"DPQE"`) काढण्यासाठी खालील कृती पूर्ण करा.
A(Δ PQF) = 20 एकक, PF = 2 DP, DP = x मानू. ∴ PF = 2x
DF = DP + `square` = `square` + `square` = 3x
Δ FDE व Δ FPQ मध्ये
∠ FDE ≅ ∠`square` (संगत कोन)
∠ FED ≅ ∠`square` (संगत कोन)
∴ Δ FDE ∼ Δ FPQ .............(कोको कसोटी)
∴ `("A"(Δ"FDE"))/("A"(Δ"FPQ")) = square/square = ((3"x")^2)/((2"x")^2) = 9/4`
A(Δ FDE) = `9/4` × A(Δ FPQ ) = `9/4 xx square = square`
A(`square` DPQE) = A(Δ FDE) - A(Δ FPQ)
= `square - square`
= `square`
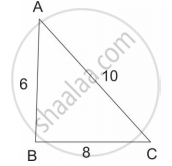
आकृतीमधील त्रिकोण समरूप आहेत का? असतील तर कोणत्या कसोटीनुसार?
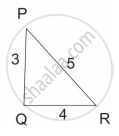
आकृतीचे निरीक्षण करून त्रिकोण समरूप आहेत का ते ठरवा. असल्यास समरूपता कसोटी लिहा. ∠P = 35°, ∠X = 35° व ∠Q = 60°, ∠Y = 60°
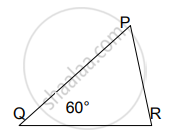
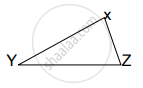
आकृतीचे निरीक्षण करा. ∆ABC व ∆PQR कोणत्या कसोटीनुसार समरूप आहेत? कसोटीचे नाव लिहा.

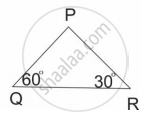
जर ΔABC ∼ ΔDEF आणि ∠A = 48°, तर ∠D = ______.

वरील आकृतीत, ΔABC मध्ये रेख XY || बाजू AC, जर 2AX = 3BX आणि XY = 9, तर AC ची किंमत काढा.
