Advertisements
Advertisements
Question
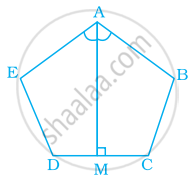
ABCDE is a regular pentagon. The bisector of angle A meets the side CD at M. Find ∠AMC.
Advertisements
Solution
Given, A pentagoan ABCDE.
The line segment AM is the bisector of the ∠A.
Now, Since the measure of each interior angle of a regular pentagon is 108°.
∴ ∠BAM = `1/2 xx 108^circ` = 54°
By the angle sum property of a quadrilateral, we have (in quadrilateral ABCM)
∠BAM + ∠ABC + ∠BCM + ∠AMC = 360°
⇒ 54° + 108° + 108° + ∠AMC = 360°
⇒ ∠AMC = 360° – 270°
⇒ ∠AMC = 90°
APPEARS IN
RELATED QUESTIONS
How many sides does a regular polygon have if the measure of an exterior angle is 24°?
Find the number of degrees in each exterior exterior angle of a regular pentagon.
What is the sum of all angles of a hexagon?
The sum of angles of a concave quadrilateral is ______.
The number of sides of a regular polygon whose each interior angle is of 135° is ______.
A nonagon has ______ sides.
is a polygon.
If the sum of interior angles is double the sum of exterior angles taken in an order of a polygon, then it is a hexagon.
A polygon is regular if all of its sides are equal.
A regular pentagon ABCDE and a square ABFG are formed on opposite sides of AB. Find ∠BCF.
