Advertisements
Advertisements
Question
An electron moving with a velocity of 5 × 104 ms−1 enters into a uniform electric field and acquires a uniform acceleration of 104 ms–2 in the direction of its initial motion.
(i) Calculate the time in which the electron would acquire a velocity double of its initial velocity.
(ii) How much distance the electron would cover at this time?
Solution
Here initial velocity of the electron,
u = 5 × 104 ms−1
acceleration, a = 104 ms−2
(i) v = 2u = 2 × 5 × 104 ms−1
= 10 ×104 ms
using v = u + at we get
10 × 104 = 5 × 104 + 104 × t or t = 5s
(ii) Using s = `"ut" + 1/2 "at"^2`, we get
s = `5 xx 10^4 xx 5 + 1/2 xx 10^4 xx 5^2`
= 25 × 104 + 12.5 × 104
= 37.5 × 104 m.
APPEARS IN
RELATED QUESTIONS
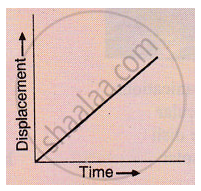
What conclusion can you draw about the velocity of a body from the displacement-time graph shown below :
A cheetah starts from, rest, and accelerates at 2 m/s2 for 10 seconds. Calculate :
(a) the final velocity
(b) the distance travelled.
Derive the formula : v = u + at, where the symbols have usual meanings.
A boy is sitting on a merry-go-round which is moving with a constant speed of 10 m s−1. This means that the boy is :
Differentiate between uniform acceleration and variable acceleration.
A bicycle initially moving with a velocity 5.0 m s-1 accelerates for 5 s at a rate of 2 m s-2. What will be its final velocity?
What do you understand by the term acceleration?
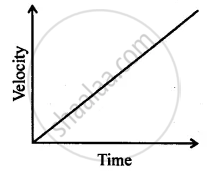
Can you suggest a real-life example about the motion of a body from the following velocity – time graph?
A packet is dropped from a stationary helicopter, hovering at a height ‘h’ from ground level, reaches the ground in 12s. Calculate
- the value of h
- final velocity of packet on reaching the ground. (Take g = 9.8 ms−2)
The velocity-time graph (Fig. 8.5) shows the motion of a cyclist. Find (i) its acceleration (ii) its velocity and (iii) the distance covered by the cyclist in 15 seconds.

