Advertisements
Advertisements
Question
An ideal gas is allowed to expand against a constant pressure of 2 bar from 10 L to 50 L in one step. Calculate the amount of work done by the gas. If the same expansion were carried out reversibly, will the work done be higher or lower than the earlier case? (Given that 1 L bar = 100 J)
Solution
We know that the amount of work done = – pextΔV
On substituting the values in the formula, we get,
– 2bar × (50 – 10) L = – 80 L bar
According to the described problem, 1 L bar = 100 J
Therefore, – 80 L bar = (– 80 × 100) = – 8000 J
= – 8 kJ, which is the amount of work done
The significance of the negative sign states that the work is done in the surroundings of the system. In the case of reversible expansion, the work done will be more.
APPEARS IN
RELATED QUESTIONS
The pressure-volume work for an ideal gas can be calculated by using the expression w = `- int_(v_i)^(v_f) p_(ex) dV`. The work can also be calculated from the pV– plot by using the area under the curve within the specified limits. When an ideal gas is compressed (a) reversibly or (b) irreversibly from volume Vi to Vf. choose the correct option.
Expansion of a gas in vacuum is called free expansion. Calculate the work done and the change in internal energy when 1 litre of ideal gas expands isothermally into vacuum until its total volume is 5 litre?
What will be the work done on an ideal gas enclosed in a cylinder, when it is compressed by a constant external pressure, pext in a single step as shown in figure. Explain graphically.
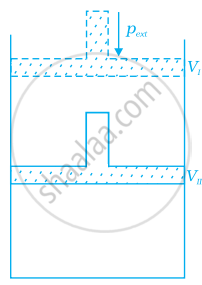
How will you calculate work done on an ideal gas in a compression, when change in pressure is carried out in infinite steps?
1.0 mol of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in figure. Calculate the work done for the expansion of gas from state (1) to state (2) at 298 K.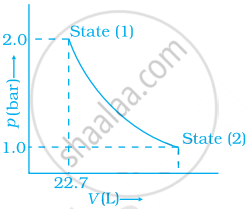
Match the following :
| A | B |
| (i) Adiabatic process | (a) Heat |
| (ii) Isolated system | (b) At constant volume |
| (iii) Isothermal change | (c) First law of thermodynamics |
| (iv) Path function | (d) No exchange of energy and matter |
| (v) State function | (e) No transfer of heat |
| (vi) ΔU = q | (f) Constant temperature |
| (vii) Law of conservation of energy | (g) Internal energy |
| (viii) Reversible process | (h) Pext = o |
| (ix) Free expansion | (i) At constant pressure |
| (x) ΔH = q | (j) Infinitely slow process which proceeds through a series of equilibrium states. |
| (xi) Intensive property | (k) Entropy |
| (xii) Extensive property | (l) Pressure |
| (m) Specific heat |
Calculate the work involved when 1 mol of an ideal gas is compressed reversibly from 1.00 bar to 5.00 bar at a constant temperature of 300 K ______.
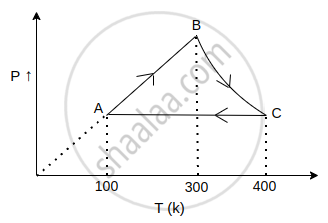
The net work done in the following cycle for one mol of an ideal gas will be ______ (in calorie), where in process BC, PT = constant. (R = 2 cal/mol-K).
Five moles of an ideal gas at 1 bar and 298 K is expanded into the vacuum to double the volume. The work done is ______.
An ideal gas expands in volume from 1 × 10−3 to 1 × 10−2 m3 at 300 K against a constant pressure of 1 × 105 Nm−2. The work done is ______.
