Question

Answer the following:

Find the trigonometric functions of :

240°

Answer 1

Trigonometric Functions of 240°: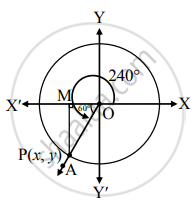

Let the measure of ∠XOA in the standard position be 240°.

Its terminal arm (ray OA) intersects the standard unit circle in P (x, y), which lies in the third quadrant.

Draw segment PM perpendicular to the X-axis.

Then OM= l x l and MP = l y l.

In right-angled triangle OMP, m∠MOP = 60° and OP = 1

∴ m∠MOP = 30°

∴ OM = `1/2"OP" = 1/2 xx 1 = 1/2`

∴ | x | = `1/2`

By the distance formula,

x²+ y²= 1

∴ `(1/2)^2 + y^2` = 1

∴ `1/4 + y^2` = 1

∴ y² = `1 - 1/4 = 3/4`

∴ y = `± sqrt(3)/2 and x = ±1/2`

But P lies in the third quadrant

∴ x < 0 and y < 0

∴ x = `-1/2 and y = -sqrt(3)/2`

∴ P is `(-1/2, -sqrt(3)/2)`

∴ sin 240° = y = `-sqrt(3)/2`

cos 240° = x = `-1/2`

tan 240° = x = `y/x = ((-(sqrt(3))/2))/((-(1)/2)) = sqrt(3)`

cosec 240° = `1/y = 1/((-(sqrt(3))/2)) = -2/sqrt(3)`

sec 240° = `1/x = 1/((-(1)/2))` = – 2

cot 240° = `x/y = ((-(1)/2))/((-(sqrt(3))/2)) = 1/sqrt(3)`