Advertisements
Advertisements
Question
Answer the following question.
Two infinitely long straight wire A1 and A2 carrying currents I and 2I flowing in the same direction are kept' distance apart. Where should a third straight wire A3 carrying current 1.5 I be placed between A1 and A2 so that it experiences no net force due to A1 and A2? Does the net force acting on A3 depend on the current flowing through it?
Advertisements
Solution
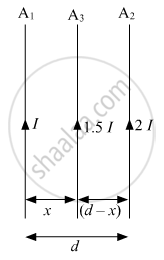
The force per unit length between two infinitely long, parallel current-carrying wires is given by:
`F = μ_0/(2pi) (I_1I_2)/d`
where:
- I1 and I2 are the currents in the wires,
- d is the separation between them,
- μ0 is the permeability of free space.
Assigning Given Values
- A1 carries current I.
- A2 carries current 2I.
- The distance between A1 and A2 is d.
- A3 carries current 1.5I and is to be placed somewhere between A1 and A2.
For A3 to experience zero net force, the magnitudes of these forces must be equal:
F1 = F2
`μ_0/(2pi) (Ixx1.5I)/x = μ_0/(2pi) (2Ixx1.5I)/((d-x)`
`(1.5I^2)/x = (3I^2)/(d-x)`
`1/x = 2/(d-x)`
d − x = 2x
d = 3x
`x = d/3`
APPEARS IN
RELATED QUESTIONS
The figure shows three infinitely long straight parallel current carrying conductors. Find the
- magnitude and direction of the net magnetic field at point A lying on conductor 1,
- magnetic force on conductor 2.
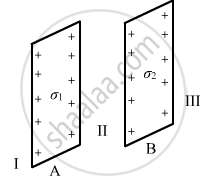
Two infinitely large plane thin parallel sheets having surface charge densities σ1 and σ2 (σ1 > σ2) are shown in the figure. Write the magnitudes and directions of the net fields in the regions marked II and III.
Figure shows a metallic wire of resistance 0.20 Ω sliding on a horizontal, U-shaped metallic rail. The separation between the parallel arms is 20 cm. An electric current of 2.0 µA passes through the wire when it is slid at a rate of 20 cm s−1. If the horizontal component of the earth's magnetic field is 3.0 × 10−5 T, calculate the dip at the place.
Two long, straight wires, each carrying a current of 5 A, are placed along the x- and y-axis respectively. The currents point along the positive directions of the axes. Find the magnetic fields at the points (a) (1 m, 1 m), (b) (−1 m, 1 m), (c) (−1 m, −1 m) and (d) (1 m, −1 m).
Four long, straight wires, each carrying a current of 5.0 A, are placed in a plane as shown in figure. The points of intersection form a square of side 5.0 cm.
(a) Find the magnetic field at the centre P of the square.
(b) Q1, Q2, Q3, and Q4, are points situated on the diagonals of the square and at a distance from P that is equal to the diagonal of the square. Find the magnetic fields at these points.
A long, straight wire carries a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. Consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the section B2 be the magnetic field at this point due to this second only. Find the value of d/l so that B2 differs from B1 by 1%.
Equal currents are passing through two very long and straight parallel wires in the same direction. They will ______
Two long straight parallel current-carrying conductors are kept ‘a’ distant apart in the air. The direction of current in both the conductors is the same. Find the magnitude of force per unit length and the direction of the force between them. Hence define one ampere.
