Advertisements
Advertisements
Question
A charged particle goes undeflected in a region containing an electric and a magnetic field. It is possible that
(a) `vecE" || "vecB , vecv" || " vec E `
(b) `vecE "is not parallel" vecB`
(c) `vecv " || " vecB but vecv "is not parallel"`
(d) `vecE" || " vecB but vecv "is not parallel"`
Solution
(a) `vecE" || "vecB , vecv" || " vec E `
(b) `vecE "is not parallel to B"`
In option (a) velocity, electric field and magnetic field are parallel to each other. So, the particle may accelerate but always continue to travel in the same straight path or go undeflected.
Another possibility of the particle to go undeviated is that magnetic force acting on it is counterbalanced by electric force. This is possible if all the three, i.e. velocity, magnetic field and electric field are perpendicular to each other, so that magnetic force is balanced by electric force. So option (b) can also be one possibility. But (c) and (d) are wrong statements.
APPEARS IN
RELATED QUESTIONS
Two infinitely long straight parallel wires, '1' and '2', carrying steady currents I1 and I2 in the same direction are separated by a distance d. Obtain the expression for the magnetic field `vecB`due to the wire '1' acting on wire '2'. Hence find out, with the help of a suitable diagram, the magnitude and direction of this force per unit length on wire '2' due to wire '1'. How does the nature of this force changes if the currents are in opposite direction? Use this expression to define the S.I. unit of current.
Using the concept of force between two infinitely long parallel current carrying conductors, define one ampere of current.
Two long straight parallel conductors 'a' and 'b', carrying steady currents Ia and Ib are separated by a distance d. Write the magnitude and direction of the magnetic field produced by the conductor 'a' at the points along the conductor 'b'. If the currents are flowing in the same direction, what is the nature and magnitude of the force between the two conductors?
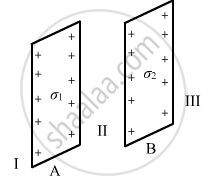
Two infinitely large plane thin parallel sheets having surface charge densities σ1 and σ2 (σ1 > σ2) are shown in the figure. Write the magnitudes and directions of the net fields in the regions marked II and III.
Derive the expression for force per unit length between two long straight parallel current carrying conductors. Hence define one ampere.
An electron beam projected along the positive x-axis deflects along the positive y-axis. If this deflection is caused by a magnetic field, what is the direction of the field? Can we conclude that the field is parallel to the z-axis?
Two parallel, long wires carry currents i1 and i2 with i1 > i2. When the currents are in the same direction, the magnetic field at a point midway between the wires is 10 µT. If the direction of i2 is reversed, the field becomes 30 µT. The ratio i1/i2 is
A long, straight wire carries a current along the z-axis, One can find two points in the x−y plane such that
(a) the magnetic fields are equal
(b) the directions of the magnetic fields are the same
(c) the magnitudes of the magnetic fields are equal
(d) the field at one point is opposite to that at the other point.
A copper wire of diameter 1.6 mm carries a current of 20 A. Find the maximum magnitude of the magnetic field `vecB` due to this current.
A straight wire of length l can slide on two parallel plastic rails kept in a horizontal plane with a separation d. The coefficient of friction between the wire and the rails is µ. If the wire carries a current i, what minimum magnetic field should exist in the space in order to slide the wire on the rails?
The magnetic field existing in a region is given by `vecB = B_0(1 + x/1)veck` . A square loop of edge l and carrying a current i, is placed with its edges parallel to the x−y axes. Find the magnitude of the net magnetic force experienced by the loop.
Figure shows a metallic wire of resistance 0.20 Ω sliding on a horizontal, U-shaped metallic rail. The separation between the parallel arms is 20 cm. An electric current of 2.0 µA passes through the wire when it is slid at a rate of 20 cm s−1. If the horizontal component of the earth's magnetic field is 3.0 × 10−5 T, calculate the dip at the place.
Two parallel wires separated by a distance of 10 cm carry currents of 10 A and 40 A along the same direction. Where should a third current by placed so that it experiences no magnetic force?
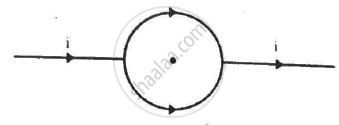
A conducting circular loop of radius a is connected to two long, straight wires. The straight wires carry a current i as shown in figure. Find the magnetic field B at the centre of the loop.
If a current I is flowing in a straight wire parallel to x-axis and magnetic field is there in the y-axis then, ______.
The nature of parallel and anti-parallel currents are ______.
Do magnetic forces obey Newton’s third law. Verify for two current elements dl1 = dlî located at the origin and dl2 = dlĵ located at (0, R, 0). Both carry current I.
Two long straight parallel conductors carrying currents I1 and I2 are separated by a distance d. If the currents are flowing in the same direction, show how the magnetic field produced by one exerts an attractive force on the other. Obtain the expression for this force and hence define 1 ampere.
Two long parallel wires kept 2 m apart carry 3A current each, in the same direction. The force per unit length on one wire due to the other is ______.
