Advertisements
Advertisements
प्रश्न
Answer the following question.
Two infinitely long straight wire A1 and A2 carrying currents I and 2I flowing in the same direction are kept' distance apart. Where should a third straight wire A3 carrying current 1.5 I be placed between A1 and A2 so that it experiences no net force due to A1 and A2? Does the net force acting on A3 depend on the current flowing through it?
उत्तर
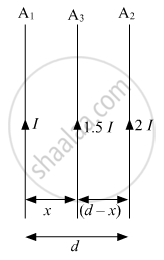
The force per unit length between two infinitely long, parallel current-carrying wires is given by:
`F = μ_0/(2pi) (I_1I_2)/d`
where:
- I1 and I2 are the currents in the wires,
- d is the separation between them,
- μ0 is the permeability of free space.
Assigning Given Values
- A1 carries current I.
- A2 carries current 2I.
- The distance between A1 and A2 is d.
- A3 carries current 1.5I and is to be placed somewhere between A1 and A2.
For A3 to experience zero net force, the magnitudes of these forces must be equal:
F1 = F2
`μ_0/(2pi) (Ixx1.5I)/x = μ_0/(2pi) (2Ixx1.5I)/((d-x)`
`(1.5I^2)/x = (3I^2)/(d-x)`
`1/x = 2/(d-x)`
d − x = 2x
d = 3x
`x = d/3`
APPEARS IN
संबंधित प्रश्न
Using the concept of force between two infinitely long parallel current carrying conductors, define one ampere of current.
Derive the expression for force per unit length between two long straight parallel current carrying conductors. Hence define one ampere.
and ```vecE` and `vecB`denote electric and magnetic fields in a frame S and `vecE`→ and `vecB` in another frame S' moving with respect to S at a velocity `vecV` Two of the following equations are wrong. Identify them.
(a) `B_y^, = B_y + (vE_z)/c^2`
(b) `E_y^' = E_y - (vB_z)/(c^2)`
`(c) Ey = By + vE_z`
`(d) E_y = E_y + vB_z`
A long, straight wire of radius r carries a current i and is placed horizontally in a uniform magnetic field B pointing vertically upward. The current is uniformly distributed over its cross section. (a) At what points will the resultant magnetic field have maximum magnitude? What will be the maximum magnitude? (b) What will be the minimum magnitude of the resultant magnetic field?
Figure shows two parallel wires separated by a distance of 4.0 cm and carrying equal currents of 10 A along opposite directions. Find the magnitude of the magnetic field B at the points A1, A2, A3.

Two long, straight wires, each carrying a current of 5 A, are placed along the x- and y-axis respectively. The currents point along the positive directions of the axes. Find the magnetic fields at the points (a) (1 m, 1 m), (b) (−1 m, 1 m), (c) (−1 m, −1 m) and (d) (1 m, −1 m).
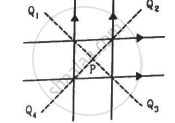
Four long, straight wires, each carrying a current of 5.0 A, are placed in a plane as shown in figure. The points of intersection form a square of side 5.0 cm.
(a) Find the magnetic field at the centre P of the square.
(b) Q1, Q2, Q3, and Q4, are points situated on the diagonals of the square and at a distance from P that is equal to the diagonal of the square. Find the magnetic fields at these points.
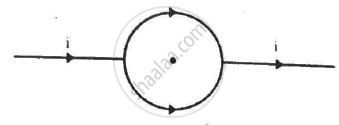
A conducting circular loop of radius a is connected to two long, straight wires. The straight wires carry a current i as shown in figure. Find the magnetic field B at the centre of the loop.
Do magnetic forces obey Newton’s third law. Verify for two current elements dl1 = dlî located at the origin and dl2 = dlĵ located at (0, R, 0). Both carry current I.
The figure below are two long, parallel wires carrying current in the same direction such that I1 < I2.
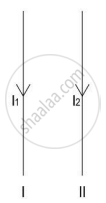
- In which direction will wire I1 move?
- If the direction of the current I2 is reversed, in which direction will the wire I1 move now?
