Advertisements
Advertisements
Question
As the temperature is increased, the time period of a pendulum ______.
Options
increases as its effective length increases even though its centre of mass still remains at the centre of the bob.
decreases as its effective length increases even though its centre of mass still remains at the centre of the bob.
increases as its effective length increases due to shifting of centre of mass below the centre of the bob.
decreases as its effective length remains same but the centre of mass shifts above the centre of the bob.
Solution
As the temperature is increased, the time period of a pendulum increases as its effective length increases even though its centre of mass still remains at the centre of the bob.
Explanation:
A pendulum clock keeps proper time at temperature θ0. If the temperature is increased to θ (> θ0), then due to linear expansion, the length of pendulum increases and hence its time period will increase
Let T = `2πsqrt(L_0/g)` at temperature θ0
And T' = `2πsqrt(L/g)` at temperature θ.
`T^'/T = sqrt(L^'/L)`
= `sqrt((L[1 + αΔθ])/L`
= `1 + 1/2 αΔθ`
Therefore change (loss or gain) in time per unit time lapsed is `(T^' - T)/T = 1/2 αΔθ`
Fractional change in time period `(ΔT)/T = 1/2 αΔθ`
So, as the temperature increases, the length of pendulum increases and hence time period of the pendulum increases. Due to an increment in its time period, a pendulum clock becomes slow in summer and will lose time.
APPEARS IN
RELATED QUESTIONS
Answer the following question.
State applications of thermal expansion.
A metal sphere 10.01 cm in diameter is placed on a brass ring of internal diameter 10 cm and at the same temperature of 12° C. The temperature up to which they should be heated together so that the metal sphere just passes through the ring is `[alpha_"metal"= 12 xx 10^-6//°"C" and alpha_"brass" =18 xx 10^-6//°"C"]` ____________.
A hot body at a temperature 'T' is kept in a surrounding of temperature 'T0'. It takes time 't1' to cool from 'T' to 'T2', time t2 to cool from 'T2' to 'T3' and time 't3' to cool from 'T3' to 'T4'. If (T - T2) = (T2 - T3) = (T3 - T4), then ______.
The radius of a metal sphere at room temperature T is R, and the coefficient of linear expansion of the metal is α. The sphere is heated a little by a temperature ∆T so that its new temperature is T + ∆T. The increase in the volume of the sphere is approximately ______.
A student records the initial length l, change in temperature ∆T and change in length ∆l of a rod as follows:
| S.No. | l(m) | ∆T (C) | ∆l (m) |
| 1. | 2 | 10 | `4 xx 10^-4` |
| 2. | 1 | 10 | `4 xx 10^-4` |
| 3. | 2 | 20 | `2 xx 10^-4` |
| 4. | 3 | 10 | `6 xx 10^-4` |
If the first observation is correct, what can you say about observations 2, 3 and 4.
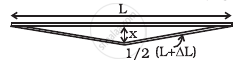
A rail track made of steel having length 10 m is clamped on a raillway line at its two ends (figure). On a summer day due to rise in temperature by 20° C, it is deformed as shown in figure. Find x (displacement of the centre) if αsteel = 1.2 × 10–5/°C.
An anisotropic material has coefficient of linear thermal expansion α1, α2 and α3 along x, y and z-axis respectively. Coefficient of cubical expansion of its material will be equal to ______.
A solid metallic cube having a total surface area of 24 m2 is uniformly heated. If its temperature is increased by 10°C, calculate the increase in the volume of the cube.
(Given: α = 5.0 × 10-4°C-1)
A glass flask is filled up to a mark with 50 cc of mercury at 18°C. If the flask and contents are heated to 38°C, how much mercury will be above the mark? (α for glass is 9 × 10-6/°C and coefficient of real expansion of mercury is 180 × 10-6/°C)
A clock with an iron pendulum keeps the correct time at 15°C. If the room temperature is 20°C, the error in seconds per day will be near ______.
(coefficient of linear expansion of iron is 1.2 × 10-5/°C)
