Advertisements
Advertisements
Question
By vector method show that the quadrilateral with vertices A (1, 2, –1), B (8, –3, –4), C (5, –4, 1), D (–2, 1, 4) is a parallelogram.
Solution
Let `bara,barb,barc and bard` be the position vectors of vertices A, B, C, D respectively
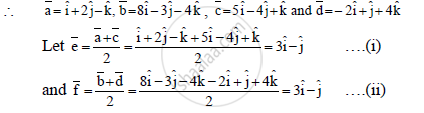
∴From (i) and (ii), we get
`bare= barf`
The mid point of the diagonals AC and BD is same
∴ The diagonals AC and BD bisect each other.
∴ The `square`ABCD is a Parallelogram.
shaalaa.com
Is there an error in this question or solution?
