HSC Science (General)
HSC Arts (English Medium)
HSC Science (Electronics)
HSC Science (Computer Science)
Academic Year: 2015-2016
Date: July 2016
Advertisements
Inverse of the statement pattern (p ∨ q) → (p ∧ q) is
(A) (p ∧ q) → (p ∨ q)
(B) ∼ (p ∨ q) → (p ∧ q)
(C) (∼ p ∨ ∼ q) → (∼ p ∧ ∼ q)
(D) (∼ p ∧ ∼ q) → (∼ p ∨ ∼ q)
Chapter: [0.01] Mathematical Logic
If the vectors `2hati-qhatj+3hatk and 4hati-5hatj+6hatk` are collinear, then value of q is
(A) 5
(B) 10
(C) 5/2
(D) 5/4
Chapter: [0.07] Vectors
If in ∆ABC with usual notations a = 18, b = 24, c = 30 then sin A/2 is equal to
(A) `1/sqrt5`
(B) `1/sqrt10`
(C) `1/sqrt15`
(D) `1/(2sqrt5)`
Chapter: [0.013000000000000001] Trigonometric Functions [0.03] Trigonometric Functions
Find the angle between the lines `barr=3hati+2hatj-4hatk+lambda(hati+2hatj+2hatk)` and `barr=5 hati-2hatk+mu(3hati+2hatj+6hatk)`
Chapter: [0.04] Pair of Straight Lines
If p, q, r are the statements with truth values T, F, T, respectively then find the truth value of (r ∧ q) ↔ ∼ p
Chapter: [0.01] Mathematical Logic [0.011000000000000001] Mathematical Logic
If `A =[[2,-3],[3,5]]` then find A-1 by adjoint method.
Chapter: [0.02] Matrices
By vector method show that the quadrilateral with vertices A (1, 2, –1), B (8, –3, –4), C (5, –4, 1), D (–2, 1, 4) is a parallelogram.
Chapter: [0.07] Vectors
Find the general solution of the equation sin x = tan x.
Chapter: [0.03] Trigonometric Functions
Find the joint equation of pair of lines passing through the origin and perpendicular to the lines represented by ax2+ 2hxy + by2= 0
Chapter: [0.04] Pair of Straight Lines
Find the principal value of `sin^-1(1/sqrt2)`
Chapter: [0.013000000000000001] Trigonometric Functions [0.03] Trigonometric Functions
Find the cartesian form of the equation of the plane `bar r=(hati+hatj)+s(hati-hatj+2hatk)+t(hati+2hatj+hatj)`
Chapter: [0.1] Plane
Simplify the following circuit so that the new circuit has minimum number of switches. Also, draw the simplified circuit.
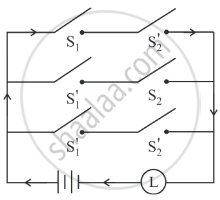
Chapter: [0.01] Mathematical Logic [0.011000000000000001] Mathematical Logic
A line makes angles of measures 45° and 60° with positive direction of y and z axes respectively. Find the d.c.s. of the line and also find the vector of magnitude 5 along the direction of line.
Chapter: [0.09] Line
Advertisements
Solve the following LPP by graphical method:
Maximize: z = 3x + 5y
Subject to: x + 4y ≤ 24
3x + y ≤ 21
x + y ≤ 9
x ≥ 0, y ≥ 0
Chapter: [0.017] Linear Programming [0.11] Linear Programming Problems
Find the shortest distance between the lines `(x+1)/7=(y+1)/(-6)=(z+1)/1 and (x-3)/1=(y-5)/(-2)=(z-7)/1`
Chapter: [0.09] Line
Show that the points (1, –1, 3) and (3, 4, 3) are equidistant from the plane 5x + 2y – 7z + 8 = 0
Chapter: [0.016] Line and Plane [0.1] Plane
In any triangle ABC with usual notations prove c = a cos B + b cos A
Chapter: [0.03] Trigonometric Functions
Find p and k if the equation px2 – 8xy + 3y2 +14x + 2y + k = 0 represents a pair of perpendicular lines.
Chapter: [0.09] Line
The cost of 4 pencils, 3 pens and 2 erasers is Rs. 60. The cost of 2 pencils, 4 pens and 6 erasers is Rs. 90 whereas the cost of 6 pencils, 2 pens and 3 erasers is Rs. 70. Find the cost of each item by using matrices.
Chapter: [0.02] Matrices
Find the volume of the parallelopiped whose coterminus edges are given by vectors `2hati+5hatj-4hatk, 5hati+7hatj+5hatk and 4hati+5hatj-2hatk`
Chapter: [0.015] Vectors [0.07] Vectors
Order and degree of the differential equation `[1+(dy/dx)^3]^(7/3)=7(d^2y)/(dx^2)` are respectively
(A) 2, 3
(B) 3, 2
(C) 7, 2
(D) 3, 7
Chapter: [0.026000000000000002] Differential Equations [0.17] Differential Equation
`∫_4^9 1/sqrtxdx=`_____
(A) 1
(B) –2
(C) 2
(D) –1
Chapter: [0.15] Integration
If the p.d.f. of a continuous random variable X is given as
`f(x)=x^2/3` for -1< x<2
=0 otherwise
then c.d.f. fo X is
(A) `x^3/9+1/9`
(B) `x^3/9-1/9`
(C) `x^2/4+1/4`
(D) `1/(9x^3)+1/9`
Chapter: [0.19] Probability Distribution
If `y = sec sqrtx` then find dy/dx.
Chapter: [0.13] Differentiation
Evaluate : `∫(x+1)/((x+2)(x+3))dx`
Chapter: [0.023] Indefinite Integration [0.15] Integration
Find the area of the region lying in the first quandrant bounded by the curve y2= 4x, X axis and the lines x = 1, x = 4
Chapter: [0.16] Applications of Definite Integral
Advertisements
For the differential equation, find the general solution:
sec2 x tan y dx + sec2 y tan x dy = 0
Chapter: [0.17] Differential Equation
Given is X ~ B(n, p). If E(X) = 6, and Var(X) = 4.2, find the value of n.
Chapter: [0.027999999999999997] Binomial Distribution [0.2] Bernoulli Trials and Binomial Distribution
If the function `f(x)=(4^sinx-1)^2/(xlog(1+2x))` for x ≠ 0 is continuous at x = 0, find f (0).
Chapter: [0.12] Continuity
Evaluate : `∫1/(3+2sinx+cosx)dx`
Chapter: [0.023] Indefinite Integration [0.15] Integration
If y = f(x) is a differentiable function of x such that inverse function x = f–1 (y) exists, then prove that x is a differentiable function of y and `dx/dy=1/((dy/dx)) " where " dy/dx≠0`
Chapter: [0.13] Differentiation
A point source of light is hung 30 feet directly above a straight horizontal path on which a man of 6 feet in height is walking. How fast will the man’s shadow lengthen and how fast will the tip of shadow move when he is walking away from the light at the rate of 100 ft/min.
Chapter: [0.14] Applications of Derivative
The probability mass function for X = number of major defects in a randomly selected
appliance of a certain type is
| X = x | 0 | 1 | 2 | 3 | 4 |
| P(X = x) | 0.08 | 0.15 | 0.45 | 0.27 | 0.05 |
Find the expected value and variance of X.
Chapter: [0.027999999999999997] Binomial Distribution [0.2] Bernoulli Trials and Binomial Distribution
Prove that `int_0^af(x)dx=int_0^af(a-x) dx`
hence evaluate `int_0^(pi/2)sinx/(sinx+cosx) dx`
Chapter: [0.15] Integration
If y = etan x+ (log x)tan x then find dy/dx
Chapter: [0.17] Differential Equation
If the probability that a fluorescent light has a useful life of at least 800 hours is 0.9, find the probabilities that among 20 such lights at least 2 will not have a useful life of at least 800 hours. [Given : (0⋅9)19 = 0⋅1348]
Chapter: [0.027000000000000003] Probability Distributions [0.19] Probability Distribution
Find a and b, so that the function f(x) defined by
f(x)=-2sin x, for -π≤ x ≤ -π/2
=a sin x+b, for -π/2≤ x ≤ π/2
=cos x, for π/2≤ x ≤ π
is continuous on [- π, π]
Chapter: [0.12] Continuity
Find the equation of a curve passing through the point (0, 2), given that the sum of the coordinates of any point on the curve exceeds the slope of the tangent to the curve at that point by 5
Chapter: [0.16] Applications of Definite Integral
If u and v are two functions of x then prove that
`intuvdx=uintvdx-int[du/dxintvdx]dx`
Hence evaluate, `int xe^xdx`
Chapter: [0.023] Indefinite Integration [0.15] Integration
Find the approximate value of log10 (1016), given that log10e = 0⋅4343.
Chapter: [0.022000000000000002] Applications of Derivatives [0.14] Applications of Derivative
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
Maharashtra State Board previous year question papers 12th Standard Board Exam Mathematics and Statistics with solutions 2015 - 2016
Previous year Question paper for Maharashtra State Board 12th Standard Board Exam Maths and Stats-2016 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics and Statistics, you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of Maharashtra State Board 12th Standard Board Exam.
How Maharashtra State Board 12th Standard Board Exam Question Paper solutions Help Students ?
• Question paper solutions for Mathematics and Statistics will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
