Advertisements
Advertisements
Question
If `A =[[2,-3],[3,5]]` then find A-1 by adjoint method.
Solution
Given `A =[[2,-3],[3,5]]`
`therefore |A| =|[2,-3],[3,5]|=10+9=19ne0`
∴A-1 exist
A11 = (-1)1+1.M11 = 5
A12 = (-1)1+2.M12 = -3
A21 = (-1)2+1.M21 = -(-3) = 3
A22 = (-1)2+2.M22 = 2
Hence, matrix of the co-factors is
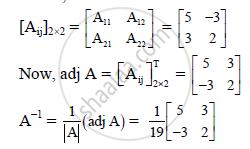
shaalaa.com
Is there an error in this question or solution?
APPEARS IN
RELATED QUESTIONS
If `A^-1=1/3[[1,4,-2],[-2,-5,4],[1,-2,1]]` and | A | = 3, then (adj. A) = _______
If `A=[[2,-2],[4,3]]` then find `A^-1` by adjoint method.
`A=[[1,2],[3,4]]` ans A(Adj A)=KI, then the value of 'K' is
If `A=[[1,-1,2],[3,0,-2],[1,0,3]]` verify that A (adj A) = |A| I.
If A = `[(2,-3),(4,1)]`, then adjoint of matrix A is
(A) `[(1,3),(-4,2)]`
(B) `[(1,-3),(-4,2)]`
(C) `[(1,3),(4,-2)]`
(D) `[(-1,-3),(-4,2)]`
