Advertisements
Advertisements
Question
C is the centre of the circle whose radius is 10 cm. Find the distance of the chord from the centre if the length of the chord is 12 cm.
Solution
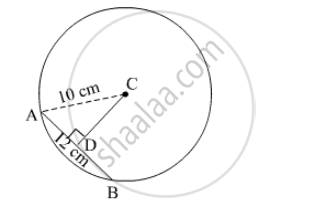
l(AC) = 10 cm
l (AB) = 12 cm
seg. CD ⊥chord AB
The perpendicular drawn from the centre of the circle to its chord bisects the chord.
∴ `l ("AD") = 1/2 l("AB")`
= `1/2 xx 12`
= 6 cm
In Δ ACD,
We apply the Pythagoras theorem
CD2 + AD2 = AC2
⇒ CD2 + 62 = 102
⇒ CD2 + 36 = 100
⇒ CD2 = 100 − 36
⇒ CD2 = 64
⇒ CD = 8 cm
Thus, the distance of the chord from the centre is 8 cm.
RELATED QUESTIONS
In a circle with centre P, chord AB is drawn of length 13 cm, seg PQ ⊥ chord AB, then find l(QB).

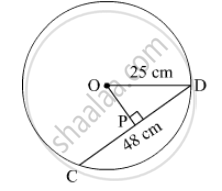
Radius of a circle with centre O is 25 cm. Find the distance of a chord from the centre if length of the chord is 48 cm.
O is centre of the circle. Find the length of radius, if the chord of length 24 cm is at a distance of 9 cm from the centre of the circle.

