Advertisements
Advertisements
Question
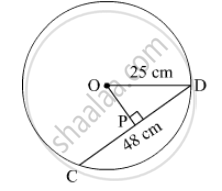
Radius of a circle with centre O is 25 cm. Find the distance of a chord from the centre if length of the chord is 48 cm.
Solution
seg OP ⊥ chord CD …[Given]
∴ l(PD) = `1/2 l(CD)` …[Perpendicular drawn from the centre of a circle to its chord bisects the chord]
∴ l(PD) = `1/2 xx 48` …[∵ l(CD) = 48 cm]
∴ l(PD) = 24 cm
In ΔOPD,
∠ OPD = 90°
∴ [l(OD)]2 = [l(OP)]2 + [l(PD)]2 … [Pythagoras theorem]
∴ (25)2 = [l(OP)]2 + (24)2
∴ (25)2 − (24)2 = [l(OP)]2
∴ 625 − 576 = [l(OP)]2
∴ 49 = [l(OP)]2
∴ l(OP) = `sqrt(49)` …[Taking square root of both sides]
∴ l(OP) = 7 cm
∴ The distance of the chord from the centre of the circle is 7 cm.
RELATED QUESTIONS
In a circle with centre P, chord AB is drawn of length 13 cm, seg PQ ⊥ chord AB, then find l(QB).

O is centre of the circle. Find the length of radius, if the chord of length 24 cm is at a distance of 9 cm from the centre of the circle.

C is the centre of the circle whose radius is 10 cm. Find the distance of the chord from the centre if the length of the chord is 12 cm.
