Advertisements
Advertisements
Question
O is centre of the circle. Find the length of radius, if the chord of length 24 cm is at a distance of 9 cm from the centre of the circle.

Solution
Join OA.
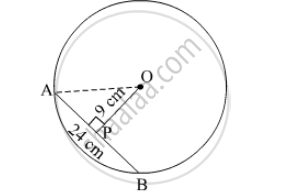
Let the perpendicular drawn from point O to the chord AB be P.
We know that the perpendicular drawn from the centre of the circle to the chord bisects the chord.
So, AP = `"AB"/2 = 24/2` = 12 cm
In Δ OPA,
We apply the Pythagoras theorem,
OP2 + AP2 = OA2
⇒ 92 + 122 = OA2
⇒ OA2 = 81 + 144 = 225
⇒ OA = `sqrt225` 15 cm
Hence, the radius of the circle is 15 cm.
RELATED QUESTIONS
In a circle with centre P, chord AB is drawn of length 13 cm, seg PQ ⊥ chord AB, then find l(QB).

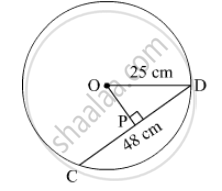
Radius of a circle with centre O is 25 cm. Find the distance of a chord from the centre if length of the chord is 48 cm.
C is the centre of the circle whose radius is 10 cm. Find the distance of the chord from the centre if the length of the chord is 12 cm.
