Advertisements
Advertisements
Question
Calculate the electric field due to a dipole on its axial line and equatorial plane.
Solution
Case (i):
Electric field due to an electric dipole at points on the axial line.
- Consider an electric dipole placed on the x-axis A point C is located at a distance of r from the midpoint of the dipole along the axial line.

Electric field of the dipole along the axial line - The electric field at a point C due to +q is
`vec"E"_+ = 1/(4 pi ε_0) "q"/("r - a")^2` (along BC) - Since the electric dipole moment vector p is from -q to +q and is directed along BC, the above equation is rewritten as
`vec"E"_+ = 1/(4 pi ε_0) "q"/("r - a")^2 hat"P"` ....(1) - 4. The electric field at a point C due to -q is
`vec"E"_- = -1/(4 pi ε_0) "q"/("r + a")^2 hat"P"` ....(2) - Since +q is located closer to the point C than -q, `vec"E"_+` is stronger than `vec"E"_-`.
Therefore, the length of the `vec"E"_+` vector is drawn larger than that of `vec"E"_-` vector.
The total electric field at point C is calculated using the superposition principle of the electric field.
`vec"E"_"tot" = vec"E"_+ + vec"E"_-`
`= 1/(4pi ε_0) "q"/("r - a")^2 hat"p" - 1/(4pi ε_0) "q"/("r + a")^2 hat"p"`
`vec"E"_"tot" = "q"/(4pi ε_0) (1/("r - a")^2 - 1/("r + a")^2)hat"p"` .....(3)
`vec"E"_"tot" = "q"/(4pi ε_0) ("4ra"/("r"^2 - "a"^2)^2) hat"p"` .....(4)
r >> a
hence (r2 - a2)2 ≈ r4
Substitute in eqn (4)
`vec"E"_"tot" = 1/(4pi ε_0)("4aq"/"r"^3)hat "p"`
`2"aq"hat"p" = vec"p"`
`vec"E"_"tot" = 1/(4pi ε_0) (2vac"p")/"r"^3` - The direction of is shown in Figure
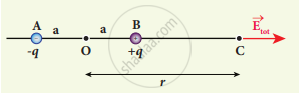
Total electric field of the dipole on the axial line
Case (ii)
- Electric field due to an electric dipole at a point on the equatorial plane.
- Consider a point C at a distance r from the midpoint 0 of the dipole on the equatorial plane.
- Since point C is equidistant from +q and -q and are the same.
- The direction of `vec"E"_+` is along BC and the direction of `vec"E"_-` is along CA.
`vec"E"_+` and `vec"E"_-` are resolved into two components; one component parallel to the dipole axis and the other perpendicular to it. - The perpendicular components `|vec"E"|` sinθ and `|vec"E"_-|` sinθ are oppositely directed and cancel each other.
`"E"_"tot" = - |"E"_+| cos theta hat "p" - |vec"E"_-| cos theta hat "p"` .....(6) - The magnitudes `vec"E"_+ and vec"E"_-` are the same and are given by
- By substituting equation (7) into equation (6) we get
`vec"E"_"tot" = - 1/(4piε_0) (2"q" cos theta)/("r"^2 + "a"^2) hat"p"`
since cos θ = `"a"/sqrt("r"^2 + "a"^2) hat`
=`- 1/(4piε_0) (2"qa")/("r"^2 +"a"^2)^(3/2) hat"p"`
since `vec"p" = "2qa"hat"p"` ....(8)
`vec"E"_"tot" = - 1/(4piε_0) vec"p"/("r"^2 +"a"^2)^(3/2)`
`|"E"_+| = |vec"E"_-| = 1/(4piε_0) "q"/("r"^2 + "a"^2)` .....(7) - At very large distances (r»a), the equation (8) becomes
`vec"E"_"tot" = - 1/(4piε_0) vec"p"/"r"^3` (r >> a)
APPEARS IN
RELATED QUESTIONS
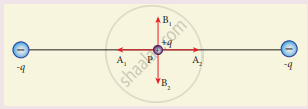
Two identical point charges of magnitude –q are fixed as shown in the figure below. A third charge +q is placed midway between the two charges at the point P. Suppose this charge +q is displaced a small distance from the point P in the directions indicated by the arrows, in which direction(s) will +q be stable with respect to the displacement?
An electric dipole is placed at an alignment angle of 30° with an electric field of 2 × 105 NC-1. It experiences a torque equal to 8 Nm. The charge on the dipole if the dipole length is lcm is ______.
Define ‘electric dipole’.
Give the expression for the magnitude of its electric dipole moment and the direction.
Write the general definition of electric dipole moment for a collection of point charge.
Derive an expression for the torque experienced by a dipole due to a uniform electric field.
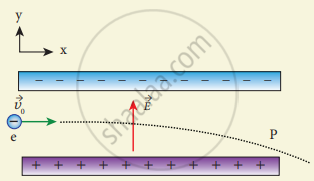
Consider an electron travelling with a speed VΦ and entering into a uniform electric field `vec"E"` which is perpendicular to `vec"V"_0` as shown in the Figure. Ignoring gravity, obtain the electron’s acceleration, velocity and position as functions of time.