Advertisements
Advertisements
Question
Derive an expression for the torque experienced by a dipole due to a uniform electric field.
Solution
- Consider an electric dipole of dipole moment `vec"p"` placed in a uniform electric field. The charge +q will experience a force q `vec"E"` in the direction of the field and charge - q `vec"E"` will experience a force -qE in a direction opposite to the field. Since the external field `vec"E"` is uniform, the total force acting on the dipole is zero.
- These two forces acting at different points will constitute a couple and the dipole experience a torque. This torque tends to rotate the dipole.
- The total torque on the dipole about the point 0, is given by
`vectau = vec"0A" xx (- "q"vec"E") + vec"0B" xx "q"vec"E"`
Torque on dipole. - Total torque is perpendicular to the plane of the paper and is directed into it. The magnitude of the total torque
`vectau = |vec"0A"| (- "q"vec"E") |sin theta + |vec"0B"| "q" vec"E"| sin theta`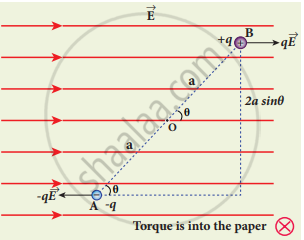
Torque on dipole
τ = qE.2a sin θ - Where θ is the angle made by `vec"p"` with `vec"E"`. Since p = 2aq, the torque is written in terms of the vector product as
`vec tau = vec"p" xx vec"E"` - The magnitude of the torque is τ = pE sin θ and is maximum when θ = 90o.
This torque tends to rotate the dipole and align it with the electric field `vec"E"`. once `vec"p"` is aligned with, the total torque on the dipole becomes zero. - If the electric field is nonuniform, then the force experienced by +q is different from that experienced by -q. In addition to the torque, there will be a net force acting on the dipole.
APPEARS IN
RELATED QUESTIONS
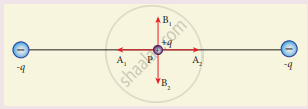
Two identical point charges of magnitude –q are fixed as shown in the figure below. A third charge +q is placed midway between the two charges at the point P. Suppose this charge +q is displaced a small distance from the point P in the directions indicated by the arrows, in which direction(s) will +q be stable with respect to the displacement?
An electric dipole is placed at an alignment angle of 30° with an electric field of 2 × 105 NC-1. It experiences a torque equal to 8 Nm. The charge on the dipole if the dipole length is lcm is ______.
Define ‘electric dipole’.
Give the expression for the magnitude of its electric dipole moment and the direction.
Write the general definition of electric dipole moment for a collection of point charge.
Calculate the electric field due to a dipole on its axial line and equatorial plane.
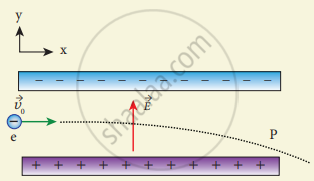
Consider an electron travelling with a speed VΦ and entering into a uniform electric field `vec"E"` which is perpendicular to `vec"V"_0` as shown in the Figure. Ignoring gravity, obtain the electron’s acceleration, velocity and position as functions of time.