Advertisements
Advertisements
Question
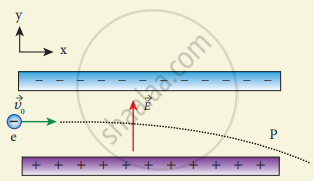
Consider an electron travelling with a speed VΦ and entering into a uniform electric field `vec"E"` which is perpendicular to `vec"V"_0` as shown in the Figure. Ignoring gravity, obtain the electron’s acceleration, velocity and position as functions of time.
Solution
Speed of an electron = V0
Uniform electric field = `vec"E"`
(а) Electron’s acceleration:
Force on electron due to uniform electric field, F = Ee
Downward acceleration of electron due to electric field, a = `"F"/"m"`
`= - "eM"/"M"`
Vector from, `vec"a" = - "eM"/"M" hat"j"`
(b) Electron’s velocity:
Speed of electron in horizontal direction, u = V0 From the equation of motion, V = u + at
V = `"V"_0 "eM"/"M" "t"`
Vector from `vec"V" = "V"_0 hat"j" - "eM"/"M" "t" hat"j"`
(c) Electron’s position:
Position of electron, s = r
From equation of motion, r = V0 t + `1/2 (- "eM"/"M")"t"^2`
r = V0 t + `1/2 "eM"/"M" "t"^2 hat"j"`
Vector from,
`vec ""r" = "V"_0 "t" hat "j" 1/2 "eM"/"M" "t"^2 hat"j"`
APPEARS IN
RELATED QUESTIONS
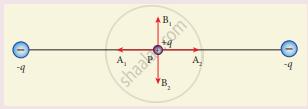
Two identical point charges of magnitude –q are fixed as shown in the figure below. A third charge +q is placed midway between the two charges at the point P. Suppose this charge +q is displaced a small distance from the point P in the directions indicated by the arrows, in which direction(s) will +q be stable with respect to the displacement?
An electric dipole is placed at an alignment angle of 30° with an electric field of 2 × 105 NC-1. It experiences a torque equal to 8 Nm. The charge on the dipole if the dipole length is lcm is ______.
Define ‘electric dipole’.
Give the expression for the magnitude of its electric dipole moment and the direction.
Write the general definition of electric dipole moment for a collection of point charge.
Calculate the electric field due to a dipole on its axial line and equatorial plane.
Derive an expression for the torque experienced by a dipole due to a uniform electric field.
