Advertisements
Advertisements
Question
Calculate the instantaneous value at 60°, average value and RMS value of an alternating current whose peak value is 20 A.
Solution
Given data:
Im = 20 A Q = 60°
i) Instantaneous value of current
i = Im sin θ
= 20 × Sin 60°
= 20 × `sqrt3/2`
= 10 × `sqrt3`
= 10 × 1.732
i = 17.32 A
ii) Average value
Iav = 0.637 Im
Iav = 0.637 × 20
= 6.37 × 2
Iav = 12.74 A
iii) Irms = 0.707 Im
= 0.707 × 20
= 7.07 × 2
Irms = 14.14 A
APPEARS IN
RELATED QUESTIONS
What are phasors?
Obtain an expression for average power of AC over a cycle. Discuss its special cases.
When does power factor of a series RLC circuit become maximum?
If Im is the maximum current, then the average value of power dissipated in a resistance R over a cycle is ______.
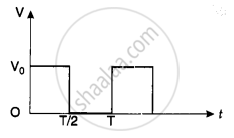
The rms value of potential difference V shown in the figure is ______.
Which of the following is independent of the frequency of a.c?
The r.m.s. value of alternating current is 10 A, having frequency of 50 Hz. The time taken by the current to increase from zero to maximum and the maximum value of current will be ______.
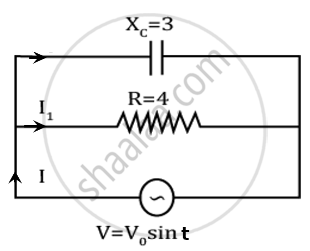
A capacitor and resistor are connected with an AC source as shown in figure. Reactance of capacitor is XC = 3 Ω and resistance of resistor is 4 Ω. Phase difference between current I and I1 is approx ______.
A direct current of 4 A and an alternating current of peak value 4 A flow through resistance of 3Ω and 2Ω respectively. The ratio of heat produced in the two resistances in same interval of time will be ______.
A 220V, 50Hz ac source is connected to a coil having coefficient of self-induction of 1H and a resistance of 400 Ω. Calculate:
- the reactance of the coil.
- the impedance of the coil.
- the current flowing through the coil.
