Question

Change the order of integration of `int_0^1int_(-sqrt(2y-y^2))^(1+sqrt(1-y^2)) f(x,y)dxdy`

Answer 1

Let `int_0^1int_(-sqrt(2y-y^2))^(1+sqrt(1-y^2)) f(x,y)dxdy`

Region of integration : `-sqrt(2y-y^2)`≤ 𝒙 ≤ 𝟏+`sqrt(1-y^2)`

𝟎≤𝒚≤ 1

Curves : (i) `x=-sqrt(2y-y^2) => x^2+y^2=2y  =>x^2+(y-1)^2=1`

Circle with centre (0,1) and radius 1.

(ii) `x=1+sqrt(1-y^2) =>  (x-1)^2+y^2=1`

Circle with centre (1,0) and radius 1.

(iii) 𝒚=𝟎 𝒍𝒊𝒏𝒆 𝒊.𝒆 𝒆𝒒𝒖𝒂𝒕𝒊𝒐𝒏 𝒐𝒇 𝒙−𝒂𝒙𝒊𝒔.
(iv) 𝒚=𝟏 𝒍𝒊𝒏𝒆 𝒑𝒂𝒓𝒂𝒍𝒍𝒆𝒍 𝒕𝒐 𝒙−𝒂𝒙𝒊𝒔.

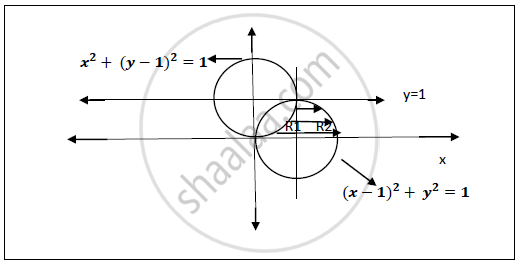
Divide the region R into R1 and R2
∴ R = R1 ∪ R2
After changing the order of integration ,
For region R1 : 𝟎≤𝒚≤𝟏−`sqrt(1-x^2)`

𝟎≤𝒙≤𝟏
For region R2 : 0 ≤𝒚≤ `sqrt(1-(x-1)^2)`

𝟏 ≤ 𝒙 ≤ 𝟐

As the region is divided in two parts the integration will be the union of the two region limits.

 `"I"=int_0^1int_0^(1-sqrt(1-x^2)) f(x,y)dydx+int_1^2int_0^(sqrt(1-(x-1)^2))f(x,y)dydx`

This is the integration after changing order from dx dy to dy dx of given integration region.