Question

Change the order of Integration and evaluate `int_0^2int_sqrt(2y)^2 x^2/(sqrtx^4-4y^2)dxdy`

Answer 1

Let I = `int_0^2int_sqrt(2y)^2 x^2/(sqrtx^4-4y^2)dxdy`
Region of integration : `sqrt(2y)<=x<=2`

`0<=y<=2`

Curves : (i) x = 2 , y = 2 , y = 0 are lines.
(ii) `x=sqrt(2y)=>x^2=2y`

Parabola with vertex (0,0) opening in upward direction.

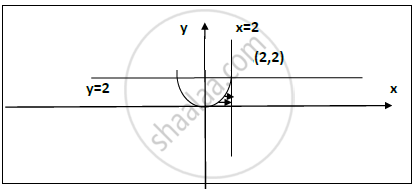
After changing the order of integration:

`0<=y<=x^2/2`

`0<=x<=2`

`therefore "I"=int_0^2int_0^(x^2/2)x^2/sqrt(x^4-4y^2)dydx`

`=1/2int_0^2int_0^(x^2/2)x^2/sqrt(x^4/4-y^2)dydx`

`=1/2int_0^2x^2[sin^(-1)(y/(x^2/2))]_0^(x^2/2)dy`

`therefore  "I"=1/2int_0^2x^2pi/2dx`

`=pi/4[x^3/3]_0^2`

`therefore "I"=(2x)/3`