Advertisements
Advertisements
Question
Chord AB and chord CD of a circle with centre 0 are congruent. If m(arc AB) = 120°, then find the m(arc CD).
Solution
Given, Chord AB = Chord CD
m(arc AB) = 120°
We know that,
arc AB ≅ arc CD ......[Corresponding arcs of congruent chord of a circle are congruent]
∴ m(arc AB) = m(arc CD)
120° = m(arc CD)
∴ m(arc CD) = 120°
RELATED QUESTIONS
In the given figure, ∆QRS is an equilateral triangle. Prove that,
- arc RS ≅ arc QS ≅ arc QR
- m(arc QRS) = 240°.

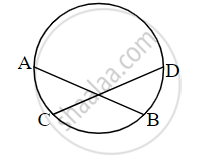
In the given figure, chord AB ≅ chord CD, Prove that, arc AC ≅ arc BD.
Four alternative answers for the following question is given. Choose the correct alternative
In a cyclic ▢ABCD, twice the measure of ∠A is thrice the measure of ∠C. Find the measure of ∠C?
Four alternative answers for the following question is given. Choose the correct alternative.
Points A, B, C are on a circle, such that m(arc AB) = m(arc BC) = 120°. No point, except point B, is common to the arcs. Which is the type of ∆ABC?
`square`PQRS is a parallelogram. Write the sum of measures of ∠P and ∠ Q.
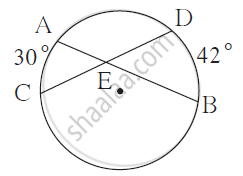
From the information given in the figure, find the measure of ∠ AEC.
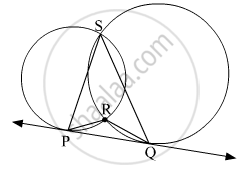
In the given figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P, Q.
Prove that, ∠ PRQ + ∠ PSQ = 180°
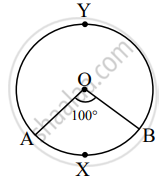
In the figure given above, O is the centre of the circle. Using given information complete the following table:
| Type of arc | Name of the arc | Measure of the arc |
| Minor arc | `square` | `square` |
| Major arc | `square` | `square` |
What is the measure of a semi circular arc?
In figure, in a circle with center O, the length of chord AB is equal to the radius of the circle. Find the measure of the following.
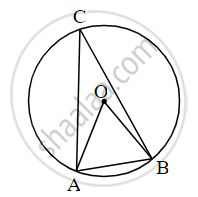
(i) ∠AOB
(ii) ∠ACB
(iii) arc AB.
In the figure, quadrilateral ABCD is cyclic. If m(arc BC) = 90° and ∠DBC = 55°, then find the measure of ∠BCD.