Advertisements
Advertisements
Question
Co-ordinates of origin are ______.
Options
(0, 0)
(0, 1)
(1, 0)
(1, 1)
Solution
Co-ordinates of origin are (0, 0).
Explanation:
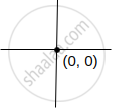
APPEARS IN
RELATED QUESTIONS
The coordinates of the point P are (−3, 2). Find the coordinates of the point Q which lies on the line joining P and origin such that OP = OQ.
Find the value of x such that PQ = QR where the coordinates of P, Q and R are (6, -1), (1, 3) and (x, 8) respectively.
Show hat A(1,2), B(4,3),C(6,6) and D(3,5) are the vertices of a parallelogram. Show that ABCD is not rectangle.
Find the area of a quadrilateral ABCD whose vertices area A(3, -1), B(9, -5) C(14, 0) and D(9, 19).
If the vertices of ΔABC be A(1, -3) B(4, p) and C(-9, 7) and its area is 15 square units, find the values of p
The distance of the point P (4, 3) from the origin is
If P ( 9a -2 , - b) divides the line segment joining A (3a + 1 , - 3 ) and B (8a, 5) in the ratio 3 : 1 , find the values of a and b .
Write the condition of collinearity of points (x1, y1), (x2, y2) and (x3, y3).
A line segment is of length 10 units. If the coordinates of its one end are (2, −3) and the abscissa of the other end is 10, then its ordinate is
If Points (1, 2) (−5, 6) and (a, −2) are collinear, then a =
If P is a point on x-axis such that its distance from the origin is 3 units, then the coordinates of a point Q on OY such that OP = OQ, are
f the coordinates of one end of a diameter of a circle are (2, 3) and the coordinates of its centre are (−2, 5), then the coordinates of the other end of the diameter are
The points (–5, 2) and (2, –5) lie in the ______.
The point whose ordinate is 4 and which lies on y-axis is ______.
The perpendicular distance of the point P(3, 4) from the y-axis is ______.
If the coordinate of point A on the number line is –1 and that of point B is 6, then find d(A, B).
Ryan, from a very young age, was fascinated by the twinkling of stars and the vastness of space. He always dreamt of becoming an astronaut one day. So, he started to sketch his own rocket designs on the graph sheet. One such design is given below :
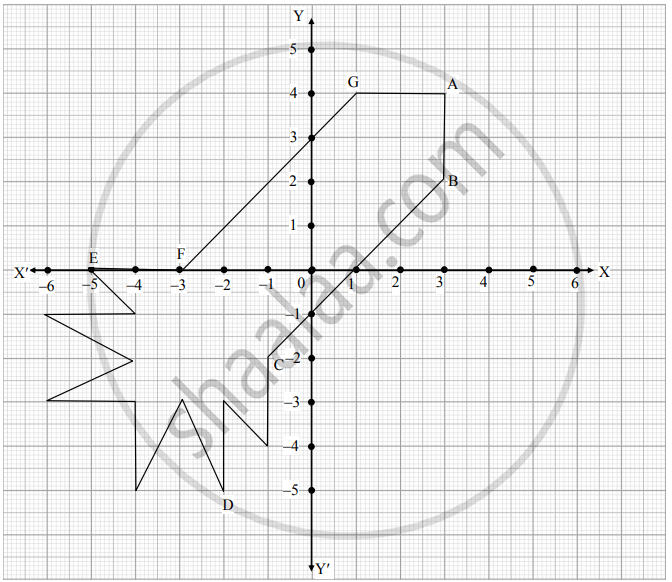
Based on the above, answer the following questions:
i. Find the mid-point of the segment joining F and G. (1)
ii. a. What is the distance between the points A and C? (2)
OR
b. Find the coordinates of the points which divides the line segment joining the points A and B in the ratio 1 : 3 internally. (2)
iii. What are the coordinates of the point D? (1)
Assertion (A): Mid-point of a line segment divides the line segment in the ratio 1 : 1
Reason (R): The ratio in which the point (−3, k) divides the line segment joining the points (− 5, 4) and (− 2, 3) is 1 : 2.
