Question

Consider a circular current-carrying loop of radius R in the x-y plane with centre at origin. Consider the line intergral

`ℑ(L ) = |int_(-L)^L B.dl|` taken along z-axis.

1. Show that ℑ(L) monotonically increases with L.
2. Use an appropriate Amperian loop to show that ℑ(∞) = µ₀I, where I is the current in the wire.
3. Verify directly the above result.
4. Suppose we replace the circular coil by a square coil of sides R carrying the same current I. What can you say about ℑ(L) and ℑ(∞)?

Answer 1

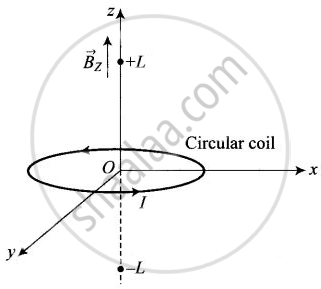
Magnetic field due to a circular current-carrying loop lying in the xy-plane acts along z-axis as shown in figure.

a. B(z) points in the same direction of z-axis and hence ℑ(L)  is monotonical function of L as B and dl are long in the same direction.

So B.dl = Bdl cos θ = Bdl cos θ° = Bdl

∴ ℑ(L)  is monotonically increasing function of L.

b. Now consider as Amperean loop around the circular coil of such a large radius that L  → `oo`. Since this loop encloses a current I, Now using Ampere's law

`ℑ(oo) = oint_(-oo)^(+oo) vec(B) * vec(dl) = mu_0I`

c. The magnetic field at the axis (z-axis) of circular coil is given by `B_z = (mu_0IR^2)/(2(z^2 + R^2)^(3/2)`

Now integrating

`int_(-oo)^(+oo) B_z dz = int_(-oo)^(+oo) (mu_0IR^2)/(2(z^2 + R^2)^(3/2)) dz`

Let z = R tan θ so that dz = R sec² θ dθ

And `(z^2 + R^2)^(3/2) = (R^2 tan^2 theta + R^2)^(3/2)`

= `R^3 sec^3θ (as  1 + tan^2θ = sec^2θ)`

Thus `int_(-oo)^(+oo) B_zdz = (mu_0I)/2 int_(- pi/2)^(+ pi/2) (R^2(R sec^2 θ dθ))/(R^3 sec^3θ)`

= `(mu_0I)/2 int_(- pi/2)^(+ pi/2) cos θ  dθ = mu_0I`

d. As we know `(B_z)_("square") < (B_z)_("circular coil")`

For the same current and side of the square equal to radius of the coil

`ℑ(oo)_("square") < ℑ(oo)_("circular coil")`

By using the same argument as we done in case (b), it can be shown that `ℑ(oo)_("square") < ℑ(oo)_("circular coil")`