Advertisements
Advertisements
Question
Consider a system of n charges q1, q2, ... qn with position vectors `vecr_1,vecr_2,vecr_3,...... vecr_n`relative to some origin 'O'. Deduce the expression for the net electric field`vec E` at a point P with position vector `vecr_p,`due to this system of charges.
Solution
Let us consider a system of n charges q1, q2, ... qn with position vectors r1, r2, r3, ...rn relative to origin O.

Let `vecF_i` be the force due to ith charge qi on q0.
Then,
`vecF_i = 1/(4πε_0) (q_1q_0)/(r_i^2) \ hat r_i`
Here, ri is the distance of the test charge q0 from qi.
The electric field at the observation point P is given by `vecE_i = lim_(q0->0) vecF_i/(q_0) = lim _(q0->0) 1/q_0 (1/(4πε_0) (q_1q_0)/r_1^2 hatr_i)`
`vecE_i = 1/(4πε_0) q_i/(r_1^2)hat r_i ........ (1) `
If `vecE` is the electric field at point P due to the system of charges, then by the principle of superposition of electric fields,
`vecE = vecE_1 +vecE_2 +vecE_3 +....vecE_n = sum_(i=1)^n vecE_i`
Using (1), we get
`vecE = sum_(i=1)^n 1/(4πε_0)q_i/(r_i^2)hat r_i `
`vecE =1/(4πε_0) sum_(i=1)^n q_i/(r_i^2)hat r_i`
APPEARS IN
RELATED QUESTIONS
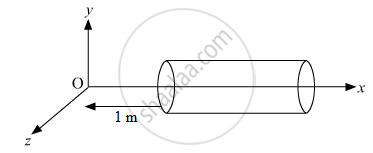
A hollow cylindrical box of length 1 m and area of cross-section 25 cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by `vecE = 50xhati` where E is NC−1 and x is in metres. Find
(i) Net flux through the cylinder.
(ii) Charge enclosed by the cylinder.
Why does a phonograph record attract dust particles just after it is cleaned?
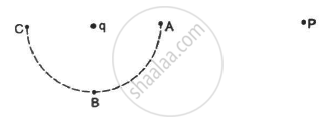
Consider the situation in the figure. The work done in taking a point charge from P to Ais WA, from P to B is WB and from P to C is WC.
A particle of mass m and charge q is thrown at a speed u against a uniform electric field E. How much distance will it travel before coming to momentary rest ?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How long will it take for the particle to travel a distance of 40 cm?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How much is the work done by the electric force on the particle during this period?
12 J of work has to be done against an existing electric field to take a charge of 0.01 C from A to B. How much is the potential difference VB − VA?
An electric field of 20 NC−1 exists along the x-axis in space. Calculate the potential difference VB − VA where the points A and B are
(a) A = (0, 0); B = (4 m, 2m)
(b) A = (4 m, 2 m); B = (6 m, 5 m)
(c) A = (0, 0); B = (6 m, 5 m)
Do you find any relation between the answers of parts (a), (b) and (c)?
Two identical blocks are kept on a frictionless horizontal table connected by a spring of stiffness k and of original length l0. A total charge Q is distributed on the block such that maximum elongation of spring at equilibrium is equal to x. Value of Q is ______.
