Advertisements
Advertisements
Question
A particle of mass m and charge q is thrown at a speed u against a uniform electric field E. How much distance will it travel before coming to momentary rest ?
Solution
Given:
Charge of the particle = q
Velocity of projection = u
Electric field intensity = E
Mass of the particle = m
We know that the force experience by a charged particle in an electric field is qE.
Acceleration produced, a = \[\frac{qE}{m}\] (Negative because the particle is thrown against the electric field)
Let the distance covered by the particle be s.
Then v2 = u2 + 2as
[Here, a = deceleration, v = final velocity]
Here, 0 = u2 − 2as
\[\Rightarrow s = \frac{u^2}{2a}\]
\[ \Rightarrow s = \frac{m u^2}{2qE}\]
APPEARS IN
RELATED QUESTIONS
Consider a system of n charges q1, q2, ... qn with position vectors `vecr_1,vecr_2,vecr_3,...... vecr_n`relative to some origin 'O'. Deduce the expression for the net electric field`vec E` at a point P with position vector `vecr_p,`due to this system of charges.
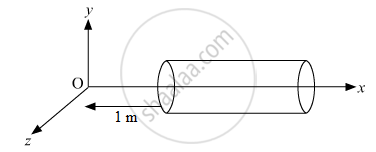
A hollow cylindrical box of length 0.5 m and area of cross-section 25 cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by `vecE = 20 xhati` where E is NC−1 and x is in metres. Find
(i) Net flux through the cylinder.
(ii) Charge enclosed by the cylinder.
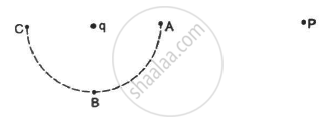
Consider the situation in the figure. The work done in taking a point charge from P to Ais WA, from P to B is WB and from P to C is WC.
A point charge q is rotated along a circle in an electric field generated by another point charge Q. The work done by the electric field on the rotating charge in one complete revolution is
Which of the following quantities does not depend on the choice of zero potential or zero potential energy?
The electric field in a region is directed outward and is proportional to the distance rfrom the origin. Taking the electric potential at the origin to be zero,
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. Find the electric force and the force of gravity acting on this particle. Can one of these forces be neglected in comparison with the other for approximate analysis?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How long will it take for the particle to travel a distance of 40 cm?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. What will be the speed of the particle after travelling this distance?
A block of mass m with a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k, as shown in the figure. A horizontal electric field E, parallel to the spring, is switched on. Find the amplitude of the resulting SHM of the block. 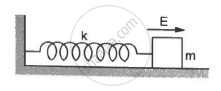
12 J of work has to be done against an existing electric field to take a charge of 0.01 C from A to B. How much is the potential difference VB − VA?
An electric field \[\vec{E} = ( \vec{i} 20 + \vec{j} 30) {NC}^{- 1}\] exists in space. If the potential at the origin is taken to be zero, find the potential at (2 m, 2 m).
The electric potential existing in space is \[\hspace{0.167em} V(x, y, z) = A(xy + yz + zx) .\] (a) Write the dimensional formula of A. (b) Find the expression for the electric field. (c) If A is 10 SI units, find the magnitude of the electric field at (1 m, 1 m, 1 m).
Find the magnitude of the electric field at the point P in the configuration shown in the figure for d >> a.
The surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the center of the disc is `sigma/(2∈_0)`. With respect to the field at the center, the electric field along the axis at a distance R from the center of the disc ______.
Consider a region inside which, there are various types of charges but the total charge is zero. At points outside the region ______.
The Electric field at a point is ______.
- always continuous.
- continuous if there is no charge at that point.
- discontinuous only if there is a negative charge at that point.
- discontinuous if there is a charge at that point.
