Advertisements
Advertisements
प्रश्न
A particle of mass m and charge q is thrown at a speed u against a uniform electric field E. How much distance will it travel before coming to momentary rest ?
उत्तर
Given:
Charge of the particle = q
Velocity of projection = u
Electric field intensity = E
Mass of the particle = m
We know that the force experience by a charged particle in an electric field is qE.
Acceleration produced, a = \[\frac{qE}{m}\] (Negative because the particle is thrown against the electric field)
Let the distance covered by the particle be s.
Then v2 = u2 + 2as
[Here, a = deceleration, v = final velocity]
Here, 0 = u2 − 2as
\[\Rightarrow s = \frac{u^2}{2a}\]
\[ \Rightarrow s = \frac{m u^2}{2qE}\]
APPEARS IN
संबंधित प्रश्न
The figure shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

An infinite line charge produces a field of 9 × 104 N/C at a distance of 2 cm. Calculate the linear charge density.
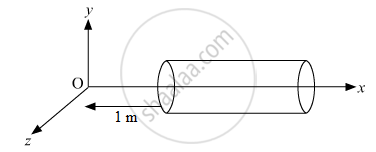
A hollow cylindrical box of length 0.5 m and area of cross-section 25 cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by `vecE = 20 xhati` where E is NC−1 and x is in metres. Find
(i) Net flux through the cylinder.
(ii) Charge enclosed by the cylinder.
The charge on a proton is +1.6 × 10−19 C and that on an electron is −1.6 × 10−19 C. Does it mean that the electron has 3.2 × 10−19 C less charge than the proton?
Why does a phonograph record attract dust particles just after it is cleaned?
In some old texts it is mentioned that 4π lines of force originate from each unit positive charge. Comment on the statement in view of the fact that 4π is not an integer.
If a body is charged by rubbing it, its weight
A point charge q is rotated along a circle in an electric field generated by another point charge Q. The work done by the electric field on the rotating charge in one complete revolution is
Electric potential decreases uniformly from 120 V to 80 V, as one moves on the x-axis from x = −1 cm to x = +1 cm. The electric field at the origin
(a) must be equal to 20 Vcm−1
(b) may be equal to 20 Vcm−1
(c) may be greater than 20 Vcm−1
(d) may be less than 20 Vcm−1
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. Find the electric force and the force of gravity acting on this particle. Can one of these forces be neglected in comparison with the other for approximate analysis?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How long will it take for the particle to travel a distance of 40 cm?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. What will be the speed of the particle after travelling this distance?
An electric field \[\vec{E} = ( \vec{i} 20 + \vec{j} 30) {NC}^{- 1}\] exists in space. If the potential at the origin is taken to be zero, find the potential at (2 m, 2 m).
Find the magnitude of the electric field at the point P in the configuration shown in the figure for d >> a.
The surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the center of the disc is `sigma/(2∈_0)`. With respect to the field at the center, the electric field along the axis at a distance R from the center of the disc ______.
Two identical blocks are kept on a frictionless horizontal table connected by a spring of stiffness k and of original length l0. A total charge Q is distributed on the block such that maximum elongation of spring at equilibrium is equal to x. Value of Q is ______.
