Advertisements
Advertisements
प्रश्न
An electric field \[\vec{E} = ( \vec{i} 20 + \vec{j} 30) {NC}^{- 1}\] exists in space. If the potential at the origin is taken to be zero, find the potential at (2 m, 2 m).
उत्तर
Given:
\[\vec{E} = ( \vec{i} 20 + \vec{j} 30) \] N/C
\[\vec{r} = (2 \vec{i} + 2 \vec{j} )\]
So,
\[V = - \vec{E} . \vec{r}\]
\[\Rightarrow V = - ( \vec{i} 20 + 30 \vec{j} ) . (2 \vec{i} + 2 \vec{j} )\]
\[ \Rightarrow V = - (2 \times 20 + 2 \times 30) = - 100\] V
APPEARS IN
संबंधित प्रश्न
Consider a system of n charges q1, q2, ... qn with position vectors `vecr_1,vecr_2,vecr_3,...... vecr_n`relative to some origin 'O'. Deduce the expression for the net electric field`vec E` at a point P with position vector `vecr_p,`due to this system of charges.
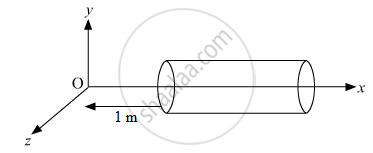
A hollow cylindrical box of length 1 m and area of cross-section 25 cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by `vecE = 50xhati` where E is NC−1 and x is in metres. Find
(i) Net flux through the cylinder.
(ii) Charge enclosed by the cylinder.
Can a gravitational field be added vectorially to an electric field to get a total field?
In some old texts it is mentioned that 4π lines of force originate from each unit positive charge. Comment on the statement in view of the fact that 4π is not an integer.
When the separation between two charges is increased, the electric potential energy of the charges
The electric field at the origin is along the positive x-axis. A small circle is drawn with the centre at the origin, cutting the axes at points A, B, C and D with coordinates (a, 0), (0, a), (−a, 0), (0, −a), respectively. Out of the points on the periphery of the circle, the potential is minimum at
A point charge q is rotated along a circle in an electric field generated by another point charge Q. The work done by the electric field on the rotating charge in one complete revolution is
Electric potential decreases uniformly from 120 V to 80 V, as one moves on the x-axis from x = −1 cm to x = +1 cm. The electric field at the origin
(a) must be equal to 20 Vcm−1
(b) may be equal to 20 Vcm−1
(c) may be greater than 20 Vcm−1
(d) may be less than 20 Vcm−1
Which of the following quantities does not depend on the choice of zero potential or zero potential energy?
A 10-cm long rod carries a charge of +50 μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both ends of the rod.
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How much is the work done by the electric force on the particle during this period?
A ball of mass 100 g and with a charge of 4.9 × 10−5 C is released from rest in a region where a horizontal electric field of 2.0 × 104 N C−1 exists. (a) Find the resultant force acting on the ball. (b) What will be the path of the ball? (c) Where will the ball be at the end of 2 s?
A block of mass m with a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k, as shown in the figure. A horizontal electric field E, parallel to the spring, is switched on. Find the amplitude of the resulting SHM of the block. 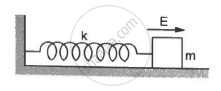
The kinetic energy of a charged particle decreases by 10 J as it moves from a point at potential 100 V to a point at potential 200 V. Find the charge on the particle.
The surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the center of the disc is `sigma/(2∈_0)`. With respect to the field at the center, the electric field along the axis at a distance R from the center of the disc ______.
Two identical blocks are kept on a frictionless horizontal table connected by a spring of stiffness k and of original length l0. A total charge Q is distributed on the block such that maximum elongation of spring at equilibrium is equal to x. Value of Q is ______.
Consider a region inside which, there are various types of charges but the total charge is zero. At points outside the region ______.
In general, metallic ropes are suspended on the carriers taking inflammable materials. The reason is ______.
The electric field intensity produced by the radiations coming from 100 W bulb at 3 m distance is E. The electric field intensity produced by the radiations coming from 50 W bulb at the same distance is:
