Advertisements
Advertisements
प्रश्न
An electric field \[\vec{E} = \vec{i}\] Ax exists in space, where A = 10 V m−2. Take the potential at (10 m, 20 m) to be zero. Find the potential at the origin.
उत्तर
Given:
Electric field intensity,
\[\vec{E} = \hat{ i } \text{Ax} = 10\text{ x } \hat{i} \]
Potential,
\[dV = - \vec{E} . \vec{\text{dx}} = - 10\text{xdx}\]
On integrating, we get
\[V = 10 \times \frac{x^2}{2} = - \left[ 5 x^2 \right]_{10}^0 \]
\[V = 5 \times 100 = 500 \] V
So, at the origin, the potential is 500 V.
APPEARS IN
संबंधित प्रश्न
An infinite line charge produces a field of 9 × 104 N/C at a distance of 2 cm. Calculate the linear charge density.
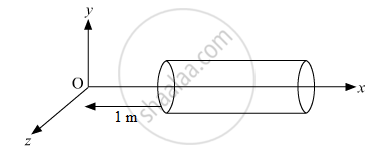
A hollow cylindrical box of length 1 m and area of cross-section 25 cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by `vecE = 50xhati` where E is NC−1 and x is in metres. Find
(i) Net flux through the cylinder.
(ii) Charge enclosed by the cylinder.
Can a gravitational field be added vectorially to an electric field to get a total field?
If a body is charged by rubbing it, its weight
A point charge q is rotated along a circle in an electric field generated by another point charge Q. The work done by the electric field on the rotating charge in one complete revolution is
The electric field and the electric potential at a point are E and V, respectively.
Electric potential decreases uniformly from 120 V to 80 V, as one moves on the x-axis from x = −1 cm to x = +1 cm. The electric field at the origin
(a) must be equal to 20 Vcm−1
(b) may be equal to 20 Vcm−1
(c) may be greater than 20 Vcm−1
(d) may be less than 20 Vcm−1
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. Find the electric force and the force of gravity acting on this particle. Can one of these forces be neglected in comparison with the other for approximate analysis?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How much is the work done by the electric force on the particle during this period?
A ball of mass 100 g and with a charge of 4.9 × 10−5 C is released from rest in a region where a horizontal electric field of 2.0 × 104 N C−1 exists. (a) Find the resultant force acting on the ball. (b) What will be the path of the ball? (c) Where will the ball be at the end of 2 s?
The electric potential existing in space is \[\hspace{0.167em} V(x, y, z) = A(xy + yz + zx) .\] (a) Write the dimensional formula of A. (b) Find the expression for the electric field. (c) If A is 10 SI units, find the magnitude of the electric field at (1 m, 1 m, 1 m).
The kinetic energy of a charged particle decreases by 10 J as it moves from a point at potential 100 V to a point at potential 200 V. Find the charge on the particle.
Find the magnitude of the electric field at the point P in the configuration shown in the figure for d >> a.
Which of the following methods can be used to charge a metal sphere positively without touching it? Select the most appropriate.
The surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the center of the disc is `sigma/(2∈_0)`. With respect to the field at the center, the electric field along the axis at a distance R from the center of the disc ______.
Two identical blocks are kept on a frictionless horizontal table connected by a spring of stiffness k and of original length l0. A total charge Q is distributed on the block such that maximum elongation of spring at equilibrium is equal to x. Value of Q is ______.
Consider a region inside which, there are various types of charges but the total charge is zero. At points outside the region ______.
When 1014 electrons are removed from a neutral metal sphere, the charge on the sphere becomes ______.
