Advertisements
Advertisements
प्रश्न
The electric potential existing in space is \[\hspace{0.167em} V(x, y, z) = A(xy + yz + zx) .\] (a) Write the dimensional formula of A. (b) Find the expression for the electric field. (c) If A is 10 SI units, find the magnitude of the electric field at (1 m, 1 m, 1 m).
उत्तर
Given:
Electric potential,
\[V(x, y, z) = A(xy + yz + zx)\]
\[A = \frac{\text{ volt }}{m^2}\]
\[ \Rightarrow \left[ A \right] = \frac{\left[ {ML}^2 I^{- 1} T^{- 3} \right]}{\left[ L^2 \right]}\]
\[ \Rightarrow A = [ {MT}^{- 3} I^{- 1} ]\]
(b) Let E be the electric field.
\[dV = - \vec{E} . \vec{dr} \]
\[ \Rightarrow A(y + z)dx + A(z + x)dy + A(x + y)dz = - E(dx \hat{i} + dy \hat{j} + dz\hat{ k } )\]
\[ \Rightarrow [A(y + z) \hat{i } + A(z + x)\hat{ j } + A(x + y) \hat{ k } ] [dx\hat{ i} + dy \hat{j } + dz \hat{k } ] = - E\left[ dx \hat{ i }+ dy\hat{ j } + dz \hat{ k } \right]\]
Equating now, we get
\[\vec{E} = - A(y + z) \hat{ i } - A(z + x) \hat{ j } - A(x + y) \hat{ k }\]
(c) Given: A = 10 V/m2
\[r = (1 m, 1 m, 1 m)\]
\[ \vec{E} = - 10 (2) \hat{ i } - 10 (2) \hat{ j } - 10 (2) \hat{ k } \]
\[ = - 20 \hat{ i } - 20 \hat{ j } - 20 \hat{ k }\]
Magnitude of electric field,
\[\left| E \right| = \sqrt{{20}^2 + {20}^2 + {20}^2}\]
\[ = \sqrt{1200} = 34 . 64 = 35\] N/C
APPEARS IN
संबंधित प्रश्न
Consider a system of n charges q1, q2, ... qn with position vectors `vecr_1,vecr_2,vecr_3,...... vecr_n`relative to some origin 'O'. Deduce the expression for the net electric field`vec E` at a point P with position vector `vecr_p,`due to this system of charges.
The charge on a proton is +1.6 × 10−19 C and that on an electron is −1.6 × 10−19 C. Does it mean that the electron has 3.2 × 10−19 C less charge than the proton?
Can a gravitational field be added vectorially to an electric field to get a total field?
Consider the situation in the figure. The work done in taking a point charge from P to Ais WA, from P to B is WB and from P to C is WC.
A point charge q is rotated along a circle in an electric field generated by another point charge Q. The work done by the electric field on the rotating charge in one complete revolution is
The electric field and the electric potential at a point are E and V, respectively.
Electric potential decreases uniformly from 120 V to 80 V, as one moves on the x-axis from x = −1 cm to x = +1 cm. The electric field at the origin
(a) must be equal to 20 Vcm−1
(b) may be equal to 20 Vcm−1
(c) may be greater than 20 Vcm−1
(d) may be less than 20 Vcm−1
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. Find the electric force and the force of gravity acting on this particle. Can one of these forces be neglected in comparison with the other for approximate analysis?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How long will it take for the particle to travel a distance of 40 cm?
A ball of mass 100 g and with a charge of 4.9 × 10−5 C is released from rest in a region where a horizontal electric field of 2.0 × 104 N C−1 exists. (a) Find the resultant force acting on the ball. (b) What will be the path of the ball? (c) Where will the ball be at the end of 2 s?
A block of mass m with a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k, as shown in the figure. A horizontal electric field E, parallel to the spring, is switched on. Find the amplitude of the resulting SHM of the block. 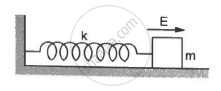
An electric field \[\vec{E} = \vec{i}\] Ax exists in space, where A = 10 V m−2. Take the potential at (10 m, 20 m) to be zero. Find the potential at the origin.
The surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the center of the disc is `sigma/(2∈_0)`. With respect to the field at the center, the electric field along the axis at a distance R from the center of the disc ______.
Two identical blocks are kept on a frictionless horizontal table connected by a spring of stiffness k and of original length l0. A total charge Q is distributed on the block such that maximum elongation of spring at equilibrium is equal to x. Value of Q is ______.
When 1014 electrons are removed from a neutral metal sphere, the charge on the sphere becomes ______.
The electric field intensity produced by the radiations coming from 100 W bulb at 3 m distance is E. The electric field intensity produced by the radiations coming from 50 W bulb at the same distance is:
The Electric field at a point is ______.
- always continuous.
- continuous if there is no charge at that point.
- discontinuous only if there is a negative charge at that point.
- discontinuous if there is a charge at that point.
