Advertisements
Advertisements
प्रश्न
A ball of mass 100 g and with a charge of 4.9 × 10−5 C is released from rest in a region where a horizontal electric field of 2.0 × 104 N C−1 exists. (a) Find the resultant force acting on the ball. (b) What will be the path of the ball? (c) Where will the ball be at the end of 2 s?
उत्तर
Given:
Charge of the ball, q = 4.9 × 10−5 C
Electrical field intensity, E = 2 × 104 N/C
Mass of the ball, m = 100 gm
Force of gravity, Fg = mg
Electrical force, Fe = Eq
The particle moves due to the resultant force of Fg and Fe.
\[R^2 = {F_g}^2 + {F_e}^2 \]
\[ = (0 . 1 \times 9 . 8 )^2 + (4 . 9 \times {10}^{- 5} \times 2 \times {10}^4 )^2 \]
\[ = 0 . 9604 + 96 . 04 \times {10}^{- 2} \]
\[ = 1 . 9208 N\]
\[ \Rightarrow R = 1 . 3859 N\]
Fg = Fe
⇒ tanθ = 1
⇒ θ = 45°
θ is the angle made by the horizontal with the resultant.
Hence, the path of the ball is straight and is along the resultant force at an angle of 45° with the horizontal
Vertical displacement in t = 2 s,
\[y = \frac{1}{2}g t^2 \]
\[ \Rightarrow y = \frac{1}{2} \times 9 . 8 \times 2 \times 2 = 19 . 6 \] m
Both the forces are same.
So, vertical displacement in 2 s = Horizontal displacement in 2 s
Net displacement
\[= \sqrt{\left( 19 . 6 \right)^2 + \left( 19 . 6 \right)^2} = \sqrt{768 . 932} = 27 . 7 \] m
APPEARS IN
संबंधित प्रश्न
The figure shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

Consider a system of n charges q1, q2, ... qn with position vectors `vecr_1,vecr_2,vecr_3,...... vecr_n`relative to some origin 'O'. Deduce the expression for the net electric field`vec E` at a point P with position vector `vecr_p,`due to this system of charges.
The electric field at the origin is along the positive x-axis. A small circle is drawn with the centre at the origin, cutting the axes at points A, B, C and D with coordinates (a, 0), (0, a), (−a, 0), (0, −a), respectively. Out of the points on the periphery of the circle, the potential is minimum at
If a body is charged by rubbing it, its weight
Consider the situation in the figure. The work done in taking a point charge from P to Ais WA, from P to B is WB and from P to C is WC.
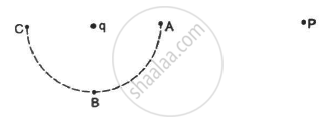
Which of the following quantities does not depend on the choice of zero potential or zero potential energy?
The electric field in a region is directed outward and is proportional to the distance rfrom the origin. Taking the electric potential at the origin to be zero,
A 10-cm long rod carries a charge of +50 μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both ends of the rod.
A wire is bent in the form of a regular hexagon and a total charge q is distributed uniformly on it. What is the electric field at the centre? You may answer this part without making any numerical calculations.
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. Find the electric force and the force of gravity acting on this particle. Can one of these forces be neglected in comparison with the other for approximate analysis?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How long will it take for the particle to travel a distance of 40 cm?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. What will be the speed of the particle after travelling this distance?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How much is the work done by the electric force on the particle during this period?
12 J of work has to be done against an existing electric field to take a charge of 0.01 C from A to B. How much is the potential difference VB − VA?
An electric field \[\vec{E} = ( \vec{i} 20 + \vec{j} 30) {NC}^{- 1}\] exists in space. If the potential at the origin is taken to be zero, find the potential at (2 m, 2 m).
Two identical blocks are kept on a frictionless horizontal table connected by a spring of stiffness k and of original length l0. A total charge Q is distributed on the block such that maximum elongation of spring at equilibrium is equal to x. Value of Q is ______.
In general, metallic ropes are suspended on the carriers taking inflammable materials. The reason is ______.
Two similar spheres having +Q and -Q charges are kept at a certain distance. F force acts between the two. If at the middle of two spheres, another similar sphere having +Q charge is kept, then it experiences a force in magnitude and direction as ______.
Five charges, q each are placed at the corners of a regular pentagon of side ‘a’ (Figure).
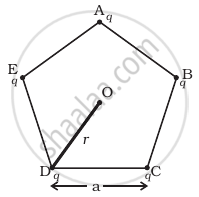
(a) (i) What will be the electric field at O, the centre of the pentagon?
(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by –q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its corners?
