Advertisements
Advertisements
Question
A ball of mass 100 g and with a charge of 4.9 × 10−5 C is released from rest in a region where a horizontal electric field of 2.0 × 104 N C−1 exists. (a) Find the resultant force acting on the ball. (b) What will be the path of the ball? (c) Where will the ball be at the end of 2 s?
Advertisements
Solution
Given:
Charge of the ball, q = 4.9 × 10−5 C
Electrical field intensity, E = 2 × 104 N/C
Mass of the ball, m = 100 gm
Force of gravity, Fg = mg
Electrical force, Fe = Eq
The particle moves due to the resultant force of Fg and Fe.
\[R^2 = {F_g}^2 + {F_e}^2 \]
\[ = (0 . 1 \times 9 . 8 )^2 + (4 . 9 \times {10}^{- 5} \times 2 \times {10}^4 )^2 \]
\[ = 0 . 9604 + 96 . 04 \times {10}^{- 2} \]
\[ = 1 . 9208 N\]
\[ \Rightarrow R = 1 . 3859 N\]
Fg = Fe
⇒ tanθ = 1
⇒ θ = 45°
θ is the angle made by the horizontal with the resultant.
Hence, the path of the ball is straight and is along the resultant force at an angle of 45° with the horizontal
Vertical displacement in t = 2 s,
\[y = \frac{1}{2}g t^2 \]
\[ \Rightarrow y = \frac{1}{2} \times 9 . 8 \times 2 \times 2 = 19 . 6 \] m
Both the forces are same.
So, vertical displacement in 2 s = Horizontal displacement in 2 s
Net displacement
\[= \sqrt{\left( 19 . 6 \right)^2 + \left( 19 . 6 \right)^2} = \sqrt{768 . 932} = 27 . 7 \] m
APPEARS IN
RELATED QUESTIONS
Show that if we connect the smaller and the outer sphere by a wire, the charge q on the former will always flow to the latter, independent of how large the charge Q is.
A point charge q is rotated along a circle in an electric field generated by another point charge Q. The work done by the electric field on the rotating charge in one complete revolution is
Electric potential decreases uniformly from 120 V to 80 V, as one moves on the x-axis from x = −1 cm to x = +1 cm. The electric field at the origin
(a) must be equal to 20 Vcm−1
(b) may be equal to 20 Vcm−1
(c) may be greater than 20 Vcm−1
(d) may be less than 20 Vcm−1
A 10-cm long rod carries a charge of +50 μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both ends of the rod.
Consider a uniformly charged ring of radius R. Find the point on the axis where the electric field is maximum.
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. What will be the speed of the particle after travelling this distance?
12 J of work has to be done against an existing electric field to take a charge of 0.01 C from A to B. How much is the potential difference VB − VA?
Consider the situation of the previous problem. A charge of −2.0 × 10−4 C is moved from point A to point B. Find the change in electrical potential energy UB − UA for the cases (a), (b) and (c).
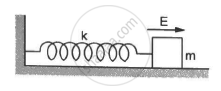
The kinetic energy of a charged particle decreases by 10 J as it moves from a point at potential 100 V to a point at potential 200 V. Find the charge on the particle.
Find the magnitude of the electric field at the point P in the configuration shown in the figure for d >> a.
Which of the following methods can be used to charge a metal sphere positively without touching it? Select the most appropriate.
The surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the center of the disc is `sigma/(2∈_0)`. With respect to the field at the center, the electric field along the axis at a distance R from the center of the disc ______.
Consider a region inside which, there are various types of charges but the total charge is zero. At points outside the region ______.
Two similar spheres having +Q and -Q charges are kept at a certain distance. F force acts between the two. If at the middle of two spheres, another similar sphere having +Q charge is kept, then it experiences a force in magnitude and direction as ______.
The electric field intensity produced by the radiations coming from 100 W bulb at 3 m distance is E. The electric field intensity produced by the radiations coming from 50 W bulb at the same distance is:
The Electric field at a point is ______.
- always continuous.
- continuous if there is no charge at that point.
- discontinuous only if there is a negative charge at that point.
- discontinuous if there is a charge at that point.
Five charges, q each are placed at the corners of a regular pentagon of side ‘a’ (Figure).
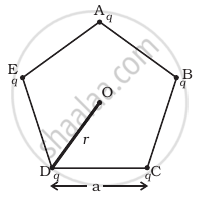
(a) (i) What will be the electric field at O, the centre of the pentagon?
(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by –q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its corners?
