Advertisements
Advertisements
Question
The bob of a simple pendulum has a mass of 40 g and a positive charge of 4.0 × 10−6 C. It makes 20 oscillations in 45 s. A vertical electric field pointing upward and of magnitude 2.5 × 104 NC−1 is switched on. How much time will it now take to complete 20 oscillations?
Solution
Given:
Charge of the particle, q = 4.0 × 10−6 C
Electrical field intensity, E = 2.5 × 104 NC−1
Mass of the particle, m = 40 g = 0.04 kg
When no electrical field is applied,
time period,
\[T_1 = 2\pi\sqrt{\frac{l}{g}}\]
When upward electrical field is applied,
time period,
\[T_2 = 2\pi\sqrt{\frac{l}{g - a}}\],
where a is the upward acceleration due to electrical field, which is given by
\[a = \frac{qE}{m}\]
\[ \Rightarrow a = \frac{4 \times {10}^{- 6} \times 2 . 5 \times {10}^4}{40 \times {10}^{- 3}}\]
\[ = 2 . 5 \text{m/ s}^2 \]
\[\therefore \frac{T_2}{T_1} = \sqrt{\frac{g}{g - a}}\]
\[ \Rightarrow \frac{T_2}{T_1} = \sqrt{\frac{9 . 8}{9 . 8 - 2 . 5}}\]
\[ \Rightarrow T_2 = 45 \times \sqrt{\frac{9 . 8}{7 . 3}} = 52 \] s
APPEARS IN
RELATED QUESTIONS
A charge is distributed uniformly over a ring of radius 'a'. Obtain an expression for the electric intensity E at a point on the axis of the ring. Hence, show that for points at large distance from the ring, it behaves like a point charge.
What is the amount of work done in moving a point charge Q around a circular arc of radius ‘r’ at the centre of which another point charge ‘q’ is located?
Why must electrostatic field at the surface of a charged conductor be normal to the surface at every point? Give reason?
The intensity of the electric field at a point at a perpendicular distance ‘r’ from an infinite line charge, having linear charge density ‘λ’ is given by:
A charged oil drop weighing 1.6 x 10-15 N is found to remain suspended in a uniform electric field of intensity 2 x 103 Nc-1. Find the charge on the drop.
A solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ = kra, where k and a are constants and r is the distance from its centre. If the electric field at r = `"R"/2` is `1/8` times that at r = R, the value of a is ______.
An electron falls from rest through a vertical distance h in a uniform and vertically upward directed electric field E. The direction of electric field is now reversed, keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h. The time of fall of the electron, in comparison to the time of fall of the proton is ______.
Assertion: On moving a distance two times the initial distance away from an infinitely long straight uniformly charged wire the electric field reduces to one-third of the initial value.
Reason: The electric field is inversely proportional to the distance from an infinitely long straight uniformly charged wire.
A particle of charge q and mass m moves rectilinearly under the action of electric field E = A – Bx, where A and B are positive constants and x is distance from the point where particle was initially at rest then the distance traveled by the particle before coming to rest and acceleration of particle at that moment are respectively.
Let there be a spherically symmetric charge distribution with charge density varying as `rho("r") = rho_0(5/4 - "r"/"R")` upto r = R, and `rho("r") = 0` for r > R, where r is the distance from the origin. The electric field at a distance r(r < R) from the origin is given by _________.
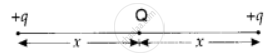
A charge Q is placed at the centre of the line joining two point charges +q and +q as shown in the figure. The ratio of charges Q and q is ______.
Electric lines of force about negative point charge are ______
A charge of 4 × 10- 9c is distributed uniformly over the circumference of a conducting ring of radius 0.3 m. Calculate the field intensity at a point on the axis of the ring at 0.4 m from its center and also at the center?
Consider two identical point charges located at points (0, 0) and (a, 0).
Is there a point on the line joining them at which the electric potential is zero?
An isolated point charge particle produces an electric field `vecE` at a point 3 m away from it. The distance of the point at which the field is `vecE/4` will be ______.
