Advertisements
Advertisements
प्रश्न
A 10-cm long rod carries a charge of +50 μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both ends of the rod.
उत्तर
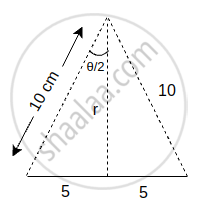
E = `(2"k"λ)/("r")sin θ/2`
`sin θ/2 = 5/10 = 1/2`
`θ/2 = 30`
E = `2 xx 9 xx 10^9 xx 50/0.10 xx 1/2 xx sqrt(100 - 25)`
E = `2 xx 9 xx 10^9 xx 50/0.10 xx 1/2 xx sqrt75`
E = `2 xx 9 xx 10^9 xx 50/0.10 xx 1/2 xx 5sqrt3`
E = 5.2 × 107 V/m
APPEARS IN
संबंधित प्रश्न
An infinite line charge produces a field of 9 × 104 N/C at a distance of 2 cm. Calculate the linear charge density.
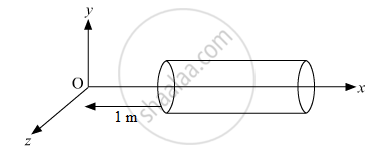
A hollow cylindrical box of length 1 m and area of cross-section 25 cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by `vecE = 50xhati` where E is NC−1 and x is in metres. Find
(i) Net flux through the cylinder.
(ii) Charge enclosed by the cylinder.
Why does a phonograph record attract dust particles just after it is cleaned?
When the separation between two charges is increased, the electric potential energy of the charges
A wire is bent in the form of a regular hexagon and a total charge q is distributed uniformly on it. What is the electric field at the centre? You may answer this part without making any numerical calculations.
A particle of mass m and charge q is thrown at a speed u against a uniform electric field E. How much distance will it travel before coming to momentary rest ?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How long will it take for the particle to travel a distance of 40 cm?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. What will be the speed of the particle after travelling this distance?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How much is the work done by the electric force on the particle during this period?
A block of mass m with a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k, as shown in the figure. A horizontal electric field E, parallel to the spring, is switched on. Find the amplitude of the resulting SHM of the block. 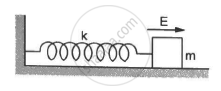
An electric field \[\vec{E} = ( \vec{i} 20 + \vec{j} 30) {NC}^{- 1}\] exists in space. If the potential at the origin is taken to be zero, find the potential at (2 m, 2 m).
An electric field \[\vec{E} = \vec{i}\] Ax exists in space, where A = 10 V m−2. Take the potential at (10 m, 20 m) to be zero. Find the potential at the origin.
The kinetic energy of a charged particle decreases by 10 J as it moves from a point at potential 100 V to a point at potential 200 V. Find the charge on the particle.
Two identical blocks are kept on a frictionless horizontal table connected by a spring of stiffness k and of original length l0. A total charge Q is distributed on the block such that maximum elongation of spring at equilibrium is equal to x. Value of Q is ______.
Consider a region inside which, there are various types of charges but the total charge is zero. At points outside the region ______.
In general, metallic ropes are suspended on the carriers taking inflammable materials. The reason is ______.
Five charges, q each are placed at the corners of a regular pentagon of side ‘a’ (Figure).
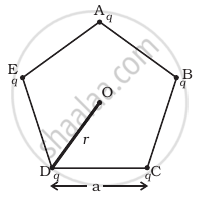
(a) (i) What will be the electric field at O, the centre of the pentagon?
(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by –q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its corners?
