Advertisements
Advertisements
प्रश्न
The electric potential existing in space is \[\hspace{0.167em} V(x, y, z) = A(xy + yz + zx) .\] (a) Write the dimensional formula of A. (b) Find the expression for the electric field. (c) If A is 10 SI units, find the magnitude of the electric field at (1 m, 1 m, 1 m).
उत्तर
Given:
Electric potential,
\[V(x, y, z) = A(xy + yz + zx)\]
\[A = \frac{\text{ volt }}{m^2}\]
\[ \Rightarrow \left[ A \right] = \frac{\left[ {ML}^2 I^{- 1} T^{- 3} \right]}{\left[ L^2 \right]}\]
\[ \Rightarrow A = [ {MT}^{- 3} I^{- 1} ]\]
(b) Let E be the electric field.
\[dV = - \vec{E} . \vec{dr} \]
\[ \Rightarrow A(y + z)dx + A(z + x)dy + A(x + y)dz = - E(dx \hat{i} + dy \hat{j} + dz\hat{ k } )\]
\[ \Rightarrow [A(y + z) \hat{i } + A(z + x)\hat{ j } + A(x + y) \hat{ k } ] [dx\hat{ i} + dy \hat{j } + dz \hat{k } ] = - E\left[ dx \hat{ i }+ dy\hat{ j } + dz \hat{ k } \right]\]
Equating now, we get
\[\vec{E} = - A(y + z) \hat{ i } - A(z + x) \hat{ j } - A(x + y) \hat{ k }\]
(c) Given: A = 10 V/m2
\[r = (1 m, 1 m, 1 m)\]
\[ \vec{E} = - 10 (2) \hat{ i } - 10 (2) \hat{ j } - 10 (2) \hat{ k } \]
\[ = - 20 \hat{ i } - 20 \hat{ j } - 20 \hat{ k }\]
Magnitude of electric field,
\[\left| E \right| = \sqrt{{20}^2 + {20}^2 + {20}^2}\]
\[ = \sqrt{1200} = 34 . 64 = 35\] N/C
APPEARS IN
संबंधित प्रश्न
The figure shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

Can a gravitational field be added vectorially to an electric field to get a total field?
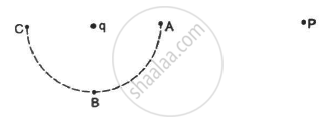
Consider the situation in the figure. The work done in taking a point charge from P to Ais WA, from P to B is WB and from P to C is WC.
Electric potential decreases uniformly from 120 V to 80 V, as one moves on the x-axis from x = −1 cm to x = +1 cm. The electric field at the origin
(a) must be equal to 20 Vcm−1
(b) may be equal to 20 Vcm−1
(c) may be greater than 20 Vcm−1
(d) may be less than 20 Vcm−1
Which of the following quantities does not depend on the choice of zero potential or zero potential energy?
A particle of mass m and charge q is thrown at a speed u against a uniform electric field E. How much distance will it travel before coming to momentary rest ?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. What will be the speed of the particle after travelling this distance?
A ball of mass 100 g and with a charge of 4.9 × 10−5 C is released from rest in a region where a horizontal electric field of 2.0 × 104 N C−1 exists. (a) Find the resultant force acting on the ball. (b) What will be the path of the ball? (c) Where will the ball be at the end of 2 s?
A block of mass m with a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k, as shown in the figure. A horizontal electric field E, parallel to the spring, is switched on. Find the amplitude of the resulting SHM of the block. 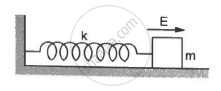
An electric field of 20 NC−1 exists along the x-axis in space. Calculate the potential difference VB − VA where the points A and B are
(a) A = (0, 0); B = (4 m, 2m)
(b) A = (4 m, 2 m); B = (6 m, 5 m)
(c) A = (0, 0); B = (6 m, 5 m)
Do you find any relation between the answers of parts (a), (b) and (c)?
An electric field \[\vec{E} = ( \vec{i} 20 + \vec{j} 30) {NC}^{- 1}\] exists in space. If the potential at the origin is taken to be zero, find the potential at (2 m, 2 m).
An electric field \[\vec{E} = \vec{i}\] Ax exists in space, where A = 10 V m−2. Take the potential at (10 m, 20 m) to be zero. Find the potential at the origin.
Assume that each atom in a copper wire contributes one free electron. Estimate the number of free electrons in a copper wire of mass 6.4 g (take the atomic weight of copper to be 64 g mol−1).
Which of the following methods can be used to charge a metal sphere positively without touching it? Select the most appropriate.
The surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the center of the disc is `sigma/(2∈_0)`. With respect to the field at the center, the electric field along the axis at a distance R from the center of the disc ______.
Two identical blocks are kept on a frictionless horizontal table connected by a spring of stiffness k and of original length l0. A total charge Q is distributed on the block such that maximum elongation of spring at equilibrium is equal to x. Value of Q is ______.
