Advertisements
Advertisements
प्रश्न
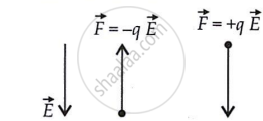
The figure shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

उत्तर
Opposite charges attract each other and the same charges repel each other. It can be observed that particles 1 and 2 both move towards the positively charged plate and repel away from the negatively charged plate. Hence, these two particles are negatively charged. It can also be observed that particle 3 moves towards the negatively charged plate and repels away from the positively charged plate. Hence, particle 3 is positively charged.
The charge to mass ratio (emf) is directly proportional to the displacement or amount of deflection for a given velocity. Since the deflection of particle 3 is the maximum, it has the highest charge to mass ratio.
APPEARS IN
संबंधित प्रश्न
Consider a system of n charges q1, q2, ... qn with position vectors `vecr_1,vecr_2,vecr_3,...... vecr_n`relative to some origin 'O'. Deduce the expression for the net electric field`vec E` at a point P with position vector `vecr_p,`due to this system of charges.
Can a gravitational field be added vectorially to an electric field to get a total field?
When the separation between two charges is increased, the electric potential energy of the charges
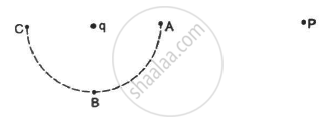
Consider the situation in the figure. The work done in taking a point charge from P to Ais WA, from P to B is WB and from P to C is WC.
The electric field and the electric potential at a point are E and V, respectively.
A 10-cm long rod carries a charge of +50 μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both ends of the rod.
A wire is bent in the form of a regular hexagon and a total charge q is distributed uniformly on it. What is the electric field at the centre? You may answer this part without making any numerical calculations.
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. What will be the speed of the particle after travelling this distance?
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How much is the work done by the electric force on the particle during this period?
A ball of mass 100 g and with a charge of 4.9 × 10−5 C is released from rest in a region where a horizontal electric field of 2.0 × 104 N C−1 exists. (a) Find the resultant force acting on the ball. (b) What will be the path of the ball? (c) Where will the ball be at the end of 2 s?
An electric field of 20 NC−1 exists along the x-axis in space. Calculate the potential difference VB − VA where the points A and B are
(a) A = (0, 0); B = (4 m, 2m)
(b) A = (4 m, 2 m); B = (6 m, 5 m)
(c) A = (0, 0); B = (6 m, 5 m)
Do you find any relation between the answers of parts (a), (b) and (c)?
An electric field \[\vec{E} = ( \vec{i} 20 + \vec{j} 30) {NC}^{- 1}\] exists in space. If the potential at the origin is taken to be zero, find the potential at (2 m, 2 m).
The electric potential existing in space is \[\hspace{0.167em} V(x, y, z) = A(xy + yz + zx) .\] (a) Write the dimensional formula of A. (b) Find the expression for the electric field. (c) If A is 10 SI units, find the magnitude of the electric field at (1 m, 1 m, 1 m).
Assume that each atom in a copper wire contributes one free electron. Estimate the number of free electrons in a copper wire of mass 6.4 g (take the atomic weight of copper to be 64 g mol−1).
The surface charge density of a thin charged disc of radius R is σ. The value of the electric field at the center of the disc is `sigma/(2∈_0)`. With respect to the field at the center, the electric field along the axis at a distance R from the center of the disc ______.
Consider a region inside which, there are various types of charges but the total charge is zero. At points outside the region ______.
In general, metallic ropes are suspended on the carriers taking inflammable materials. The reason is ______.
