Advertisements
Advertisements
प्रश्न
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How much is the work done by the electric force on the particle during this period?
उत्तर
Given:
Charge of the particle, q = 2.5 × 10−4 C
Initial velocity, u = 0
Electric field intensity, E = 1.2 × 104 N/C
Mass of the particle, m = 1 g = 10−3 kg
Distance travelled, s = 40 cm = 4 × 10−1 m
Work done by the electric force,
\[W = F_e s = 3 \times 4 \times {10}^{- 1} \]
\[ = 12 \times {10}^{- 1} \] J = 1 . 20 J
APPEARS IN
संबंधित प्रश्न
An infinite line charge produces a field of 9 × 104 N/C at a distance of 2 cm. Calculate the linear charge density.
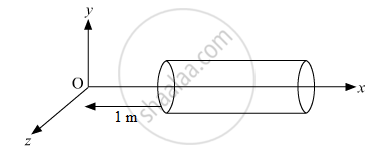
A hollow cylindrical box of length 1 m and area of cross-section 25 cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by `vecE = 50xhati` where E is NC−1 and x is in metres. Find
(i) Net flux through the cylinder.
(ii) Charge enclosed by the cylinder.
The charge on a proton is +1.6 × 10−19 C and that on an electron is −1.6 × 10−19 C. Does it mean that the electron has 3.2 × 10−19 C less charge than the proton?
Can a gravitational field be added vectorially to an electric field to get a total field?
In some old texts it is mentioned that 4π lines of force originate from each unit positive charge. Comment on the statement in view of the fact that 4π is not an integer.
If a body is charged by rubbing it, its weight
Electric potential decreases uniformly from 120 V to 80 V, as one moves on the x-axis from x = −1 cm to x = +1 cm. The electric field at the origin
(a) must be equal to 20 Vcm−1
(b) may be equal to 20 Vcm−1
(c) may be greater than 20 Vcm−1
(d) may be less than 20 Vcm−1
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. Find the electric force and the force of gravity acting on this particle. Can one of these forces be neglected in comparison with the other for approximate analysis?
A block of mass m with a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k, as shown in the figure. A horizontal electric field E, parallel to the spring, is switched on. Find the amplitude of the resulting SHM of the block. 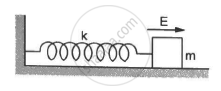
Consider the situation of the previous problem. A charge of −2.0 × 10−4 C is moved from point A to point B. Find the change in electrical potential energy UB − UA for the cases (a), (b) and (c).
The electric potential existing in space is \[\hspace{0.167em} V(x, y, z) = A(xy + yz + zx) .\] (a) Write the dimensional formula of A. (b) Find the expression for the electric field. (c) If A is 10 SI units, find the magnitude of the electric field at (1 m, 1 m, 1 m).
Which of the following methods can be used to charge a metal sphere positively without touching it? Select the most appropriate.
In general, metallic ropes are suspended on the carriers taking inflammable materials. The reason is ______.
Two similar spheres having +Q and -Q charges are kept at a certain distance. F force acts between the two. If at the middle of two spheres, another similar sphere having +Q charge is kept, then it experiences a force in magnitude and direction as ______.
The Electric field at a point is ______.
- always continuous.
- continuous if there is no charge at that point.
- discontinuous only if there is a negative charge at that point.
- discontinuous if there is a charge at that point.
Five charges, q each are placed at the corners of a regular pentagon of side ‘a’ (Figure).
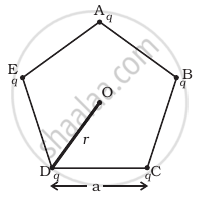
(a) (i) What will be the electric field at O, the centre of the pentagon?
(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by –q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its corners?
