Advertisements
Advertisements
प्रश्न
An electric field of 20 NC−1 exists along the x-axis in space. Calculate the potential difference VB − VA where the points A and B are
(a) A = (0, 0); B = (4 m, 2m)
(b) A = (4 m, 2 m); B = (6 m, 5 m)
(c) A = (0, 0); B = (6 m, 5 m)
Do you find any relation between the answers of parts (a), (b) and (c)?
उत्तर
Given:
Electric field intensity, E = 20 N/C
The electric field is along the x-axis. So, while calculating the potential difference between points B and A using the formula VB − VA = E.ds, we will use the difference of the x-coordinates of these point as ds.
(a) A = (0, 0) B = (4 m, 2 m).
So, VB − VA = E.ds = 20 × (0 − 4 m) = − 80 V
(b) A = (4 m, 2 m), B = (6 m, 5 m)
⇒ VB − VA = E.ds = 20 × (4 − 6) = − 40 V.
(c) A = (0, 0), B = (6 m, 5 m)
⇒ VB − VA = E.ds = 20 × (0 − 6) = − 120 V.
Potential difference between points (0, 0) and (6 m, 5 m) = Potential difference between points (0, 0) and (4 m, 2 m) + Potential difference between points (4 m, 2 m) and (6 m, 5 m)
APPEARS IN
संबंधित प्रश्न
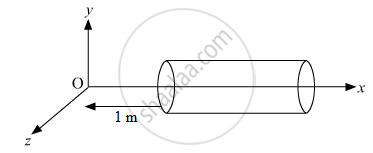
A hollow cylindrical box of length 1 m and area of cross-section 25 cm2 is placed in a three dimensional coordinate system as shown in the figure. The electric field in the region is given by `vecE = 50xhati` where E is NC−1 and x is in metres. Find
(i) Net flux through the cylinder.
(ii) Charge enclosed by the cylinder.
In some old texts it is mentioned that 4π lines of force originate from each unit positive charge. Comment on the statement in view of the fact that 4π is not an integer.
If a body is charged by rubbing it, its weight
Electric potential decreases uniformly from 120 V to 80 V, as one moves on the x-axis from x = −1 cm to x = +1 cm. The electric field at the origin
(a) must be equal to 20 Vcm−1
(b) may be equal to 20 Vcm−1
(c) may be greater than 20 Vcm−1
(d) may be less than 20 Vcm−1
Which of the following quantities does not depend on the choice of zero potential or zero potential energy?
A 10-cm long rod carries a charge of +50 μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both ends of the rod.
A wire is bent in the form of a regular hexagon and a total charge q is distributed uniformly on it. What is the electric field at the centre? You may answer this part without making any numerical calculations.
A particle of mass 1 g and charge 2.5 × 10−4 C is released from rest in an electric field of 1.2 × 10 4 N C−1. How long will it take for the particle to travel a distance of 40 cm?
A block of mass m with a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k, as shown in the figure. A horizontal electric field E, parallel to the spring, is switched on. Find the amplitude of the resulting SHM of the block. 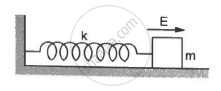
Consider the situation of the previous problem. A charge of −2.0 × 10−4 C is moved from point A to point B. Find the change in electrical potential energy UB − UA for the cases (a), (b) and (c).
The kinetic energy of a charged particle decreases by 10 J as it moves from a point at potential 100 V to a point at potential 200 V. Find the charge on the particle.
Assume that each atom in a copper wire contributes one free electron. Estimate the number of free electrons in a copper wire of mass 6.4 g (take the atomic weight of copper to be 64 g mol−1).
Which of the following methods can be used to charge a metal sphere positively without touching it? Select the most appropriate.
When 1014 electrons are removed from a neutral metal sphere, the charge on the sphere becomes ______.
The electric field intensity produced by the radiations coming from 100 W bulb at 3 m distance is E. The electric field intensity produced by the radiations coming from 50 W bulb at the same distance is:
The Electric field at a point is ______.
- always continuous.
- continuous if there is no charge at that point.
- discontinuous only if there is a negative charge at that point.
- discontinuous if there is a charge at that point.
Five charges, q each are placed at the corners of a regular pentagon of side ‘a’ (Figure).
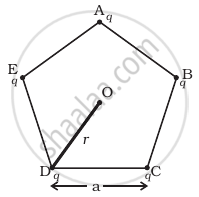
(a) (i) What will be the electric field at O, the centre of the pentagon?
(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by –q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its corners?
