Advertisements
Advertisements
Question
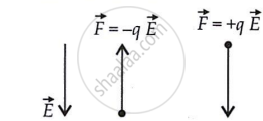
The figure shows tracks of three charged particles in a uniform electrostatic field. Give the signs of the three charges. Which particle has the highest charge to mass ratio?

Solution
Opposite charges attract each other and the same charges repel each other. It can be observed that particles 1 and 2 both move towards the positively charged plate and repel away from the negatively charged plate. Hence, these two particles are negatively charged. It can also be observed that particle 3 moves towards the negatively charged plate and repels away from the positively charged plate. Hence, particle 3 is positively charged.
The charge to mass ratio (emf) is directly proportional to the displacement or amount of deflection for a given velocity. Since the deflection of particle 3 is the maximum, it has the highest charge to mass ratio.
APPEARS IN
RELATED QUESTIONS
An infinite line charge produces a field of 9 × 104 N/C at a distance of 2 cm. Calculate the linear charge density.
When the separation between two charges is increased, the electric potential energy of the charges
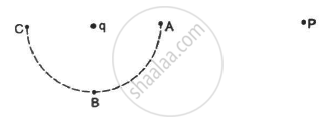
Consider the situation in the figure. The work done in taking a point charge from P to Ais WA, from P to B is WB and from P to C is WC.
Electric potential decreases uniformly from 120 V to 80 V, as one moves on the x-axis from x = −1 cm to x = +1 cm. The electric field at the origin
(a) must be equal to 20 Vcm−1
(b) may be equal to 20 Vcm−1
(c) may be greater than 20 Vcm−1
(d) may be less than 20 Vcm−1
A 10-cm long rod carries a charge of +50 μC distributed uniformly along its length. Find the magnitude of the electric field at a point 10 cm from both ends of the rod.
A block of mass m with a charge q is placed on a smooth horizontal table and is connected to a wall through an unstressed spring of spring constant k, as shown in the figure. A horizontal electric field E, parallel to the spring, is switched on. Find the amplitude of the resulting SHM of the block. 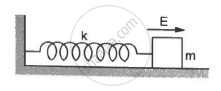
12 J of work has to be done against an existing electric field to take a charge of 0.01 C from A to B. How much is the potential difference VB − VA?
An electric field of 20 NC−1 exists along the x-axis in space. Calculate the potential difference VB − VA where the points A and B are
(a) A = (0, 0); B = (4 m, 2m)
(b) A = (4 m, 2 m); B = (6 m, 5 m)
(c) A = (0, 0); B = (6 m, 5 m)
Do you find any relation between the answers of parts (a), (b) and (c)?
Consider the situation of the previous problem. A charge of −2.0 × 10−4 C is moved from point A to point B. Find the change in electrical potential energy UB − UA for the cases (a), (b) and (c).
The kinetic energy of a charged particle decreases by 10 J as it moves from a point at potential 100 V to a point at potential 200 V. Find the charge on the particle.
Find the magnitude of the electric field at the point P in the configuration shown in the figure for d >> a.
Two identical blocks are kept on a frictionless horizontal table connected by a spring of stiffness k and of original length l0. A total charge Q is distributed on the block such that maximum elongation of spring at equilibrium is equal to x. Value of Q is ______.
Consider a region inside which, there are various types of charges but the total charge is zero. At points outside the region ______.
In general, metallic ropes are suspended on the carriers taking inflammable materials. The reason is ______.
Five charges, q each are placed at the corners of a regular pentagon of side ‘a’ (Figure).
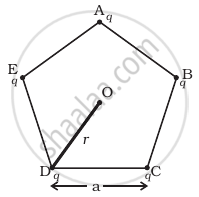
(a) (i) What will be the electric field at O, the centre of the pentagon?
(ii) What will be the electric field at O if the charge from one of the corners (say A) is removed?
(iii) What will be the electric field at O if the charge q at A is replaced by –q?
(b) How would your answer to (a) be affected if pentagon is replaced by n-sided regular polygon with charge q at each of its corners?
