Advertisements
Advertisements
Question
Consider a uniform electric field E = 3 × 103 `bbhat i` N/C.
- What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane?
- What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
Solution
- Area of square, A= a2 = 102 = 100 cm2
= 100 × 10-4 m2
= 10-2 m2
Since the plane lies on the y-z-axis, area vector `vecA` points in the same direction.
i.e., `vecA = (10^-2 hati) "m"^2`
∴ Electric Flux through the square is
Φ = `vecE · vecA`
= `(3 xx 10^3 hati) · (10^-2 hati)`
= 3 × 101
or Φ = 30 V-m - When normal to plane i.e., A makes an angle of 60° with E, then
Φ' = EA cos 60°
= 3 × 103 × 10-2 × 1/2
= 1.5 × 101
or Φ' = 15 V-m
APPEARS IN
RELATED QUESTIONS
Find out the outward flux to a point charge +q placed at the centre of a cube of side ‘a’. Why is it found to be independent of the size and shape of the surface enclosing it? Explain.
What is the net flux of the uniform electric field of previous question through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
Given a uniform electric field \[\vec{E} = 2 \times {10}^3 \ \hat{i}\] N/C, find the flux of this field through a square of side 20 cm, whose plane is parallel to the y−z plane. What would be the flux through the same square, if the plane makes an angle of 30° with the x−axis ?
Given a uniform electric filed \[\vec{E} = 4 \times {10}^3 \ \hat{i} N/C\]. Find the flux of this field through a square of 5 cm on a side whose plane is parallel to the Y-Z plane. What would be the flux through the same square if the plane makes a 30° angle with the x-axis?
Two charges of magnitudes −2Q and +Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘3a’ with its centre at the origin?
Two charges of magnitudes −3Q and + 2Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘5a’ with its centre at the origin?
A thin straight infinitely long conducting wire having charge density λ is enclosed by a cylindrical surface of radius r and length l, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
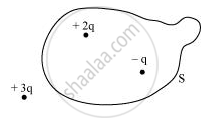
Figure shows three point charges +2q, −q and + 3q. Two charges + 2q and −q are enclosed within a surface ‘S’. What is the electric flux due to this configuration through the surface ‘S’?
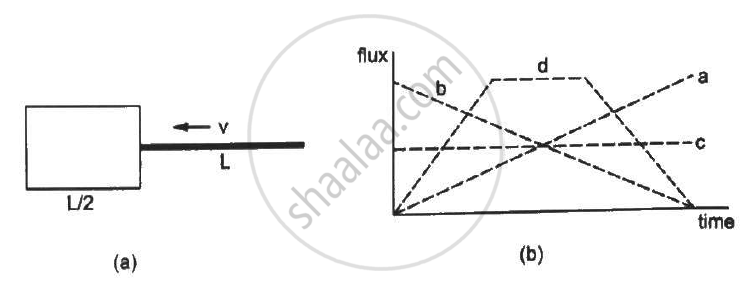
Following Figure (a) shows an imaginary cube of edge L/2. A uniformly charged rod of length (L) moves towards the left at a small but constant speed `nu.` At t = 0, the left end just touches the centre of the face of the cube opposite it. Which of the graphs shown in the figure (b) represents the flux of the electric field through the cube as the rod goes through it?
Mark the correct options:
The following figure shows a closed surface that intersects a conducting sphere. If a positive charge is placed at point P, the flux of the electric field through the closed surface

Electric charges are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10 cm surrounding the total charge is 25 V m. The flux over a concentric sphere of radius 20 cm will be _____________ .
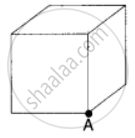
A charged particle q is placed at the centre O of cube of length L (A B C D E F G H). Another same charge q is placed at a distance L from O. Then the electric flux through ABCD is ______.
The total flux through the faces of the cube with side of length a if a charge q is placed at corner A of the cube is ______.
A point charge q is placed at a distance a/2 directly above the centre of a square of side a. The electric flux through the square is ______.
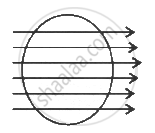
A circular disc of radius 'r' is placed along the plane of paper. A uniform electric field `vec"E"` is also present in the plane of paper. What amount of electric flux is associated with it?
The electric charges are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10 cm surrounding the total charge is 20 V-m. The flux over a concentric sphere of radius 20 cm will be ______.
