Advertisements
Advertisements
Question
Mark the correct options:
Options
Gauss's Law is valid only for symmetrical charge distributions.
Gauss's Law is valid only for charges placed in vacuum.
The electric field calculated by Gauss's Law is the field due to the charge inside the Gaussian surface.
The flux of the electric field through a closed surface due to all the charges is equal to the flux due to the charges enclosed by the surface.
Solution
The flux of the electric field through a closed surface due to all the charges is equal to the flux due to the charges enclosed by the surface.
The contribution of flux on the closed surface due to the charges lying outside the surface is zero because number of field line entering the closed surface is equal to the number of field lines coming out of the surface so the net contribution of the charge lying outside the closed surface to the flux is zero. Therefore, the net flux through the surface due to the charge lying outside the the closed surface is zero. The contribution that counts is only due to the charges lying within the closed surface.
Thus, the flux of the electric field through a closed surface due to all the charges (inside and outside the surface) is equal to the flux due to the charges enclosed by the surface
APPEARS IN
RELATED QUESTIONS
Given a uniform electric field `vecE=5xx10^3hati`N/C, find the flux of this field through a square of 10 cm on a side whose plane is parallel to the y-z plane. What would be the flux through the same square if the plane makes a 30° angle with the x-axis ?
Consider a uniform electric field E = 3 × 103 `bbhat i` N/C.
- What is the flux of this field through a square of 10 cm on a side whose plane is parallel to the yz plane?
- What is the flux through the same square if the normal to its plane makes a 60° angle with the x-axis?
What is the net flux of the uniform electric field of previous question through a cube of side 20 cm oriented so that its faces are parallel to the coordinate planes?
Two charges of magnitudes −2Q and +Q are located at points (a, 0) and (4a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘3a’ with its centre at the origin?
Two charges of magnitudes +4Q and − Q are located at points (a, 0) and (− 3a, 0) respectively. What is the electric flux due to these charges through a sphere of radius ‘2a’ with its centre at the origin?
A circular ring of radius r made of a non-conducting material is placed with its axis parallel to a uniform electric field. The ring is rotated about a diameter through 180°. Does the flux of the electric field change? If yes, does it decrease or increase?
It is said that any charge given to a conductor comes to its surface. Should all the protons come to the surface? Should all the electrons come to the surface? Should all the free electrons come to the surface?
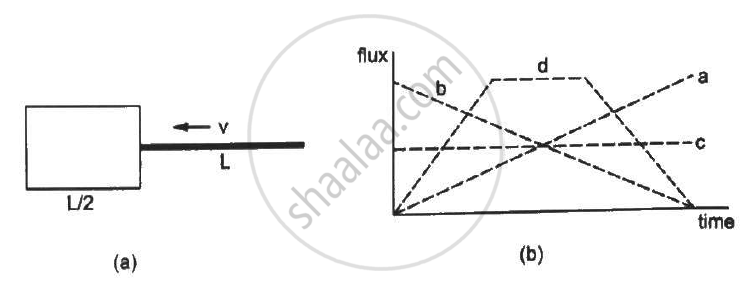
Following Figure (a) shows an imaginary cube of edge L/2. A uniformly charged rod of length (L) moves towards the left at a small but constant speed `nu.` At t = 0, the left end just touches the centre of the face of the cube opposite it. Which of the graphs shown in the figure (b) represents the flux of the electric field through the cube as the rod goes through it?
A charge q is placed at the centre of the open end of a cylindrical vessel (see the figure). The flux of the electric field through the surface of the vessel is ____________ .

If the flux of the electric field through a closed surface is zero,
(a) the electric field must be zero everywhere on the surface
(b) the electric field may be zero everywhere on the surface
(c) the charge inside the surface must be zero
(d) the charge in the vicinity of the surface must be zero
A charge 'Q' µC is placed at the centre of a cube. The flux through one face and two opposite faces of the cube is respectively ______.
The electric field intensity due to an infinite cylinder of radius R and having charge q per unit length at a distance rir r(r > R) from its axis is ______.
If the electric flux entering and leaving an enclosed surface respectively is Φ1 and Φ2, the electric charge inside the surface will be
An electric charge q is placed at the center of a cube of side ℓ. The electric flux on one of its faces will be ______.
What will be the total flux through the faces of the cube (figure) with side of length a if a charge q is placed at

- A: a corner of the cube.
- B: mid-point of an edge of the cube.
- C: centre of a face of the cube.
- D: mid-point of B and C.
A hollow sphere of radius R has a point charge Q at its centre. Electric flux emanating from it is `phi`. If both the charge and the radius of the sphere are doubled, electric flux emanating from the sphere will ______.
A hollow sphere of radius R has a point charge q at its centre. Electric flux emanating from the sphere is X. How will the electric flux change, if at all, when radius of the sphere is doubled?
