Advertisements
Online Mock Tests
Chapters
2: Kinetic Theory of Gases
3: Calorimetry
4: Laws of Thermodynamics
5: Specific Heat Capacities of Gases
6: Heat Transfer
7: Electric Field and Potential
▶ 8: Gauss’s Law
9: Capacitors
10: Electric Current in Conductors
11: Thermal and Chemical Effects of Current
12: Magnetic Field
13: Magnetic Field due to a Current
14: Permanent Magnets
15: Magnetic Properties of Matter
16: Electromagnetic Induction
17: Alternating Current
18: Electromagnetic Waves
19: Electric Current through Gases
20: Photoelectric Effect and Wave-Particle Duality
21: Bohr’s Model and Physics of Atom
22: X-rays
23: Semiconductors and Semiconductor Devices
24: The Nucleus
25: The Special Theory of Relativity
![HC Verma solutions for Concepts of Physics Vol. 2 [English] Class 11 and 12 chapter 8 - Gauss’s Law HC Verma solutions for Concepts of Physics Vol. 2 [English] Class 11 and 12 chapter 8 - Gauss’s Law - Shaalaa.com](/images/9788177092325-concepts-of-physics-vol-2-english-class-11-and-12_6:cd4e4bfcb8474a60871d8e5659ec4eb9.jpg)
Advertisements
Solutions for Chapter 8: Gauss’s Law
Below listed, you can find solutions for Chapter 8 of CBSE, Karnataka Board PUC HC Verma for Concepts of Physics Vol. 2 [English] Class 11 and 12.
HC Verma solutions for Concepts of Physics Vol. 2 [English] Class 11 and 12 8 Gauss’s Law Short Answers [Page 139]
A small plane area is rotated in an electric field. In which orientation of the area, is the flux of the electric field through the area maximum? In which orientation is it zero?
A circular ring of radius r made of a non-conducting material is placed with its axis parallel to a uniform electric field. The ring is rotated about a diameter through 180°. Does the flux of the electric field change? If yes, does it decrease or increase?
A charge Q is uniformly distributed on a spherical shell. What is the field at the centre of the shell? If a point charge is brought close to the shell, will the field at the centre change? Does your answer depend on whether the shell is conducting or non-conducting?
A spherical shell made of plastic, contains a charge Q distributed uniformly over its surface. What is the electric field inside the shell? If the shell is hammered to deshape it, without altering the charge, will the field inside be changed? What happens if the shell is made of a metal?
A point charge q is placed in a cavity in a metal block. If a charge Q is brought outside the metal, will the charge q feel an electric fore?
A rubber balloon is given a charge Q distributed uniformly over its surface. Is the field inside the balloon zero everywhere if the balloon does not have a spherical surface?
It is said that any charge given to a conductor comes to its surface. Should all the protons come to the surface? Should all the electrons come to the surface? Should all the free electrons come to the surface?
HC Verma solutions for Concepts of Physics Vol. 2 [English] Class 11 and 12 8 Gauss’s Law MCQ [Pages 139 - 140]
A charge Q is uniformly distributed over a large plastic plate. The electric field at a point P close to the centre of the plate is 10 V m−1. If the plastic plate is replaced by a copper plate of the same geometrical dimensions and carrying the same charge Q, the electric field at the point P will become
zero
5 V m−1
10 V m−1
20 V m−1
A metallic particle with no net charge is placed near a finite metal plate carrying a positive charge. The electric force on the particle will be
towards the plate
away from the plate
parallel to the plate
zero
A thin, metallic spherical shell contains a charge Q on it. A point charge q is placed at the centre of the shell and another charge q1 is placed outside it as shown in the following figure . All the three charges are positive. The force on the charge at the centre is ____________.
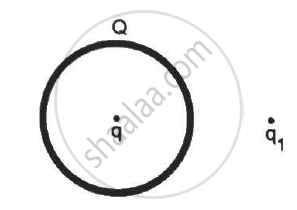
toward left
towards right
upward
zero
A thin, metallic spherical shell contains a charge Q on it. A point charge q is placed at the centre of the shell and another charge q1 is placed outside it as shown in the following figure. All the three charges are positive. The force on the central charge due to the shell is ______.
towards left
towards right
upward
zero
Electric charges are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10 cm surrounding the total charge is 25 V m. The flux over a concentric sphere of radius 20 cm will be _____________ .
a
b
c
d
Following Figure (a) shows an imaginary cube of edge L/2. A uniformly charged rod of length (L) moves towards the left at a small but constant speed `nu.` At t = 0, the left end just touches the centre of the face of the cube opposite it. Which of the graphs shown in the figure (b) represents the flux of the electric field through the cube as the rod goes through it?
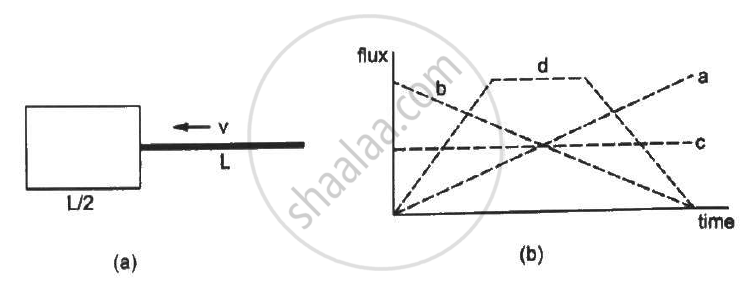
a
b
c
d
A charge q is placed at the centre of the open end of a cylindrical vessel (see the figure). The flux of the electric field through the surface of the vessel is ____________ .

zero
q/εv
q/2εv
2q/εv
HC Verma solutions for Concepts of Physics Vol. 2 [English] Class 11 and 12 8 Gauss’s Law MCQ [Pages 140 - 141]
Mark the correct options:
Gauss's Law is valid only for symmetrical charge distributions.
Gauss's Law is valid only for charges placed in vacuum.
The electric field calculated by Gauss's Law is the field due to the charge inside the Gaussian surface.
The flux of the electric field through a closed surface due to all the charges is equal to the flux due to the charges enclosed by the surface.
A positive point charge Q is brought near an isolated metal cube.
The cube becomes negatively charged.
The cube becomes positively charged.
The interior becomes positively charged and the surface becomes negatively charged.
The interior remains charge free and the surface gets non-uniform charge distribution.
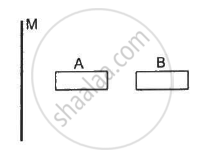
A large non-conducting sheet M is given a uniform charge density. Two uncharged small metal rods A and B are placed near the sheet as shown in the following figure.
(a) M attracts A.
(b) M attracts B.
(c) A attracts B.
(d) B attracts A.
If the flux of the electric field through a closed surface is zero,
(a) the electric field must be zero everywhere on the surface
(b) the electric field may be zero everywhere on the surface
(c) the charge inside the surface must be zero
(d) the charge in the vicinity of the surface must be zero
An electric dipole is placed at the centre of a sphere. Mark the correct options.
(a) The flux of the electric field through the sphere is zero.
(b) The electric field is zero at every point of the sphere.
(c) The electric field is not zero anywhere on the sphere.
(d) The electric field is zero on a circle on the sphere.
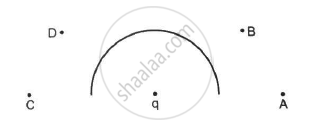
In the following figure shows a charge q placed at the centre of a hemisphere. A second charge Q is placed at one of the positions A, B, C and D. In which position(s) of this second charge, the flux of the electric field through the hemisphere remains unchanged?
(a) A
(b) B
(c) C
(d) D
A closed surface S is constructed around a conducting wire connected to a battery and a switch in the following figure. As the switch is closed, the free electrons in the wire start moving along the wire. In any time interval, the number of electrons entering the closed surface S is equal to the number of electrons leaving it. On closing the switch, the flux of the electric field through the closed surface
(a) is increased
(b) is decreased
(c) remains unchanged
(d) remains zero
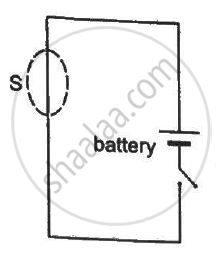
The following figure shows a closed surface that intersects a conducting sphere. If a positive charge is placed at point P, the flux of the electric field through the closed surface

will remain zero
will become positive
will become negative
will become undefined
HC Verma solutions for Concepts of Physics Vol. 2 [English] Class 11 and 12 8 Gauss’s Law Exercises [Pages 141 - 142]
The electric field in a region is given by
`vec"E"= 3/5"E"_0 vec"i" + 4/5 "E"_0 vec "i" "with" " E"_0 = 2.0 xx 10^3 "N""C"^-1.`
Find the flux of this field through a rectangular surface of area 0⋅2 m2 parallel to the y-z plane.
A charge Q is uniformly distributed over a rod of length l. Consider a hypothetical cube of edge l with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.
Show that there can be no net charge in a region in which the electric field is uniform at all points.
The electric field in a region is given by `vec"E" = ("E"_0 "x")/"l" vec"i".`
Find the charge contained inside the cubical volume bound by the surfaces
x =0, x =a, y=0, y=a, z=0 and z=a. Take
`"E"_0 = 5 xx 10^3 "N""C"^-1 , "l" =2 "cm" " and" " a" = 1 "cm" `
A charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaces of the cube.
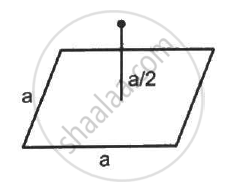
A charge Q is placed at a distance a/2 above the centre of a horizontal, square surface of edge a as shown in the following figure . Find the flux of the electric field through the square surface.
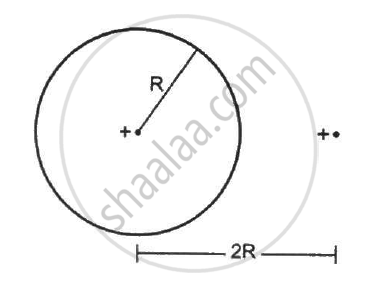
Find the flux of the electric field through a spherical surface of radius R due to a charge of 10−7 C at the centre and another equal charge at a point 2R away from the centre in the following figure.
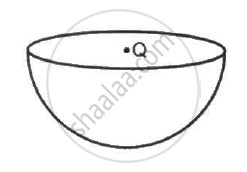
A charge Q is placed at the centre of an imaginary hemispherical surface. Using symmetry arguments and Gauss's Law, find the flux of the electric field due to this charge through the surface of the hemisphere in the following figure.
A spherical volume contains a uniformly distributed charge of density 2.0 × 10 -4 Cm-3 Find the electric field at a point inside the volume at a distance 4⋅0 cm from the centre.
The radius of a gold nucleus (Z = 79) is about 7.0 × 10-10 m. Assume that the positive charge is distributed uniformly throughout the nuclear volume. Find the strength of the electric field at (a) the surface of the nucleus and (b) at the middle point of a radius. Remembering that gold is a conductor, is it justified to assume that the positive charge is uniformly distributed over the entire volume of the nucleus and does not come to the outer surface?
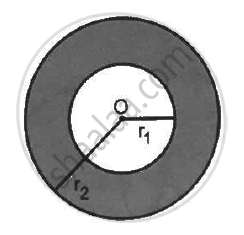
A charge Q is distributed uniformly within the material of a hollow sphere of inner and outer radii r1 and r2 (see the figure). Find the electric field at a point P at a distance x away from the centre for r1 < x < r. Draw a rough graph showing the electric field as a function of x for 0 < x < 2r2 (see the figure).
A charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius a. (a) Find the surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and outer surfaces? (c) Find the electric field inside the sphere at a distance x from the centre in the situations (a) and (b).
Consider the following very rough model of a beryllium atom. The nucleus has four protons and four neutrons confined to a small volume of radius 10−15 m. The two 1 selectrons make a spherical charge cloud at an average distance of 1⋅3 ×10−11 m from the nucleus, whereas the two 2 s electrons make another spherical cloud at an average distance of 5⋅2 × 10−11 m from the nucleus. Find three electric fields at (a) a point just inside the 1 s cloud and (b) a point just inside the 2 s cloud.
Find the magnitude of the electric field at a point 4 cm away from a line charge of density 2 × 10-6 Cm-1.
A long cylindrical wire carries a positive charge of linear density 2.0 × 10-8 C m -1 An electron revolves around it in a circular path under the influence of the attractive electrostatic force. Find the kinetic energy of the electron. Note that it is independent of the radius.
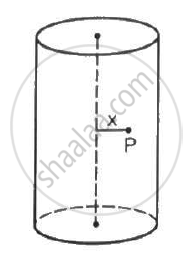
A long cylindrical volume contains a uniformly distributed charge of density ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (see the figure).
A non-conducting sheet of large surface area and thickness d contains a uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane. Draw a qualitative graph of E against x for 0 < x < d.
A charged particle with a charge of −2⋅0 × 10−6 C is placed close to a non-conducting plate with a surface charge density of 4.0 × 10-6Cm0-2. Find the force of attraction between the particle and the plate.
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical. Find the surface charge density on the plate.
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical (a) Find the tension in the string in equilibrium. (b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
Two large conducting plates are placed parallel to each other with a separation of 2⋅00 cm between them. An electron starting from rest near one of the plates reaches the other plate in 2⋅00 microseconds. Find the surface charge density on the inner surfaces.
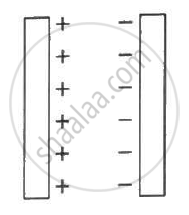
Two large conducting plates are placed parallel to each other and they carry equal and opposite charges with surface density σ as shown in the figure. Find the electric field (a) at the left of the plates (b) in between the plates and (c) at the right of the plates.
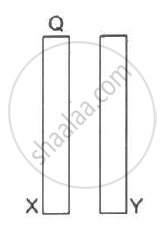
Two conducting plates X and Y, each with a large surface area A (on one side), are placed parallel to each other, as shown in the following figure . Plate X is given a charge Q,whereas the other is kept neutral. Find (a) the surface charge density at the inner surface of plate X (b) the electric field at a point to the left of the plates (c) the electric field at a point in between the plates and (d) the electric field at a point to the right of the plates.
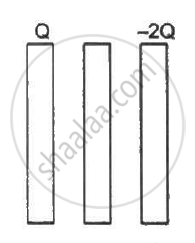
Three identical metal plates with large surface areas are kept parallel to each other as shown in the following figure. The leftmost plate is given a charge Q, the rightmost a charge −2Q and the middle one is kept neutral. Find the charge appearing on the outer surface of the rightmost plate.
Solutions for 8: Gauss’s Law
![HC Verma solutions for Concepts of Physics Vol. 2 [English] Class 11 and 12 chapter 8 - Gauss’s Law HC Verma solutions for Concepts of Physics Vol. 2 [English] Class 11 and 12 chapter 8 - Gauss’s Law - Shaalaa.com](/images/9788177092325-concepts-of-physics-vol-2-english-class-11-and-12_6:cd4e4bfcb8474a60871d8e5659ec4eb9.jpg)
HC Verma solutions for Concepts of Physics Vol. 2 [English] Class 11 and 12 chapter 8 - Gauss’s Law
Shaalaa.com has the CBSE, Karnataka Board PUC Mathematics Concepts of Physics Vol. 2 [English] Class 11 and 12 CBSE, Karnataka Board PUC solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. HC Verma solutions for Mathematics Concepts of Physics Vol. 2 [English] Class 11 and 12 CBSE, Karnataka Board PUC 8 (Gauss’s Law) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. HC Verma textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Concepts of Physics Vol. 2 [English] Class 11 and 12 chapter 8 Gauss’s Law are Electric Field Due to a System of Charges, Introduction of Electric Field, Continuous Distribution of Charges, Coulomb’s Law - Force Between Two Point Charges, Basic Properties of Electric Charge, Electric Charges, Conductors and Insulators, Superposition Principle - Forces Between Multiple Charges, Physical Significance of Electric Field, Electric Field Lines, Electric Flux, Electric Dipole, Dipole in a Uniform External Field, Gauss’s Law, Applications of Gauss’s Law, Charging by Induction, Electric Field Due to a Point Charge, Uniformly Charged Infinite Plane Sheet and Uniformly Charged Thin Spherical Shell (Field Inside and Outside), Superposition Principle of Forces, Force Between Two Point Charges.
Using HC Verma Concepts of Physics Vol. 2 [English] Class 11 and 12 solutions Gauss’s Law exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in HC Verma Solutions are essential questions that can be asked in the final exam. Maximum CBSE, Karnataka Board PUC Concepts of Physics Vol. 2 [English] Class 11 and 12 students prefer HC Verma Textbook Solutions to score more in exams.
Get the free view of Chapter 8, Gauss’s Law Concepts of Physics Vol. 2 [English] Class 11 and 12 additional questions for Mathematics Concepts of Physics Vol. 2 [English] Class 11 and 12 CBSE, Karnataka Board PUC, and you can use Shaalaa.com to keep it handy for your exam preparation.
