Advertisements
Advertisements
Question
A charge Q is placed at the centre of an imaginary hemispherical surface. Using symmetry arguments and Gauss's Law, find the flux of the electric field due to this charge through the surface of the hemisphere in the following figure.
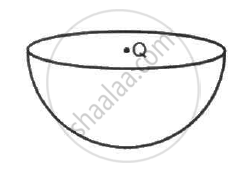
Solution
From Guass's law, flux through a closed surface, `phi = "Q"_("e""n")/∈_0,`
where
Qen = charge enclosed by the closed surface
Let us assume that a spherical closed surface in which the charge is enclosed is Q.
The flux through the sphere,
`phi = "Q"/∈_0`
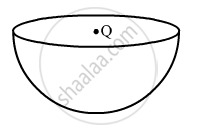
Hence for a hemisphere(open bowl), total flux through its curved surface,
`phi′ = "Q"/∈_0 xx 1/2 = "Q"/(2∈_0)`
APPEARS IN
RELATED QUESTIONS
plot a graph showing the variation of current density (j) versus the electric field (E) for two conductors of different materials. What information from this plot regarding the properties of the conducting material, can be obtained which can be used to select suitable materials for use in making (i) standard resistance and (ii) connecting wires in electric circuits?
Plot a graph showing the variation of resistivity of a conductor with temperature.
A metallic particle with no net charge is placed near a finite metal plate carrying a positive charge. The electric force on the particle will be
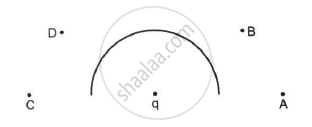
In the following figure shows a charge q placed at the centre of a hemisphere. A second charge Q is placed at one of the positions A, B, C and D. In which position(s) of this second charge, the flux of the electric field through the hemisphere remains unchanged?
(a) A
(b) B
(c) C
(d) D
Show that there can be no net charge in a region in which the electric field is uniform at all points.
The electric field in a region is given by
`vec"E"= 3/5"E"_0 vec"i" + 4/5 "E"_0 vec "i" "with" " E"_0 = 2.0 xx 10^3 "N""C"^-1.`
Find the flux of this field through a rectangular surface of area 0⋅2 m2 parallel to the y-z plane.
The electric field in a region is given by `vec"E" = ("E"_0 "x")/"l" vec"i".`
Find the charge contained inside the cubical volume bound by the surfaces
x =0, x =a, y=0, y=a, z=0 and z=a. Take
`"E"_0 = 5 xx 10^3 "N""C"^-1 , "l" =2 "cm" " and" " a" = 1 "cm" `
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical (a) Find the tension in the string in equilibrium. (b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
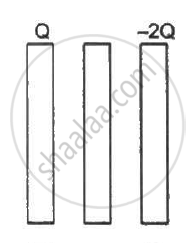
Three identical metal plates with large surface areas are kept parallel to each other as shown in the following figure. The leftmost plate is given a charge Q, the rightmost a charge −2Q and the middle one is kept neutral. Find the charge appearing on the outer surface of the rightmost plate.
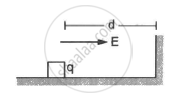
A block of mass containing a net positive charge q is placed on a smooth horizontal table which terminates in a vertical wall as shown in the figure. The distance of the block from the wall is d. A horizontal electric field E towards the right is switched on. Assuming elastic collisions (if any), find the time period of the resulting oscillatory motion. Is it a simple harmonic motion?
Consider a circular ring of radius r, uniformly charged with linear charge density λ. Find the electric potential at a point on the axis at a distance x from the centre of the ring. Using this expression for the potential, find the electric field at this point.
A uniform field of 2.0 NC−1 exists in space in the x-direction. (a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z). (b) At which point, the potential is 25 V? (c) If the potential at the origin is taken to be 100 V, what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero? Is it practical to choose the potential at infinity to be zero?
Draw equipotential surfaces corresponding to a uniform electric field in the z-directions.
Answer the following question.
Prove that the average energy density of the oscillating electric field is equal to that of the oscillating magnetic field.
When a comb rubbed with dry hair attracts pieces of paper. This is because the ______.
The force per unit charge is known as ______.
Pick out the statement which is incorrect
