Advertisements
Advertisements
Question
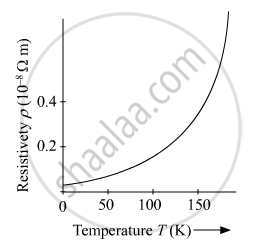
Plot a graph showing the variation of resistivity of a conductor with temperature.
Solution
The resistivity of a metallic conductor is given by
\[\rho = \rho_0 \left[ 1 + \alpha\left( T - T_0 \right) \right]\]
\\text { [where }\]
\[ \rho_0 = \text { Resistivity at reference temperature }\]
\[ T_0 =\text { Reference temperature }\]
\[ \alpha = \text { Coefficient of resistivity }\]
From the above relation, we can say that the graph between resistivity of a conductor with temperature is a straight line. But, at temperatures much lower than 273 K ( i.e. \[0 °C\], the graph deviates considerably from a straight line as shown below.
APPEARS IN
RELATED QUESTIONS
Why is the potential inside a hollow spherical charged conductor constant and has the same value of as on its surface?
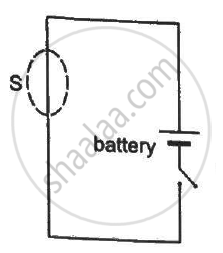
A closed surface S is constructed around a conducting wire connected to a battery and a switch in the following figure. As the switch is closed, the free electrons in the wire start moving along the wire. In any time interval, the number of electrons entering the closed surface S is equal to the number of electrons leaving it. On closing the switch, the flux of the electric field through the closed surface
(a) is increased
(b) is decreased
(c) remains unchanged
(d) remains zero
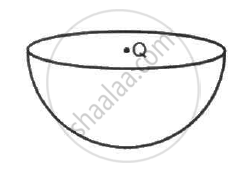
A charge Q is placed at the centre of an imaginary hemispherical surface. Using symmetry arguments and Gauss's Law, find the flux of the electric field due to this charge through the surface of the hemisphere in the following figure.
Consider the following very rough model of a beryllium atom. The nucleus has four protons and four neutrons confined to a small volume of radius 10−15 m. The two 1 selectrons make a spherical charge cloud at an average distance of 1⋅3 ×10−11 m from the nucleus, whereas the two 2 s electrons make another spherical cloud at an average distance of 5⋅2 × 10−11 m from the nucleus. Find three electric fields at (a) a point just inside the 1 s cloud and (b) a point just inside the 2 s cloud.
A charged particle with a charge of −2⋅0 × 10−6 C is placed close to a non-conducting plate with a surface charge density of 4.0 × 10-6Cm0-2. Find the force of attraction between the particle and the plate.
One end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and a charge of 4.0× 10-6 C. In equilibrium, the thread makes an angle of 60° with the vertical (a) Find the tension in the string in equilibrium. (b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
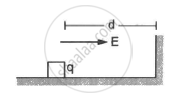
A block of mass containing a net positive charge q is placed on a smooth horizontal table which terminates in a vertical wall as shown in the figure. The distance of the block from the wall is d. A horizontal electric field E towards the right is switched on. Assuming elastic collisions (if any), find the time period of the resulting oscillatory motion. Is it a simple harmonic motion?
When a comb rubbed with dry hair attracts pieces of paper. This is because the ______.
