Advertisements
Advertisements
प्रश्न
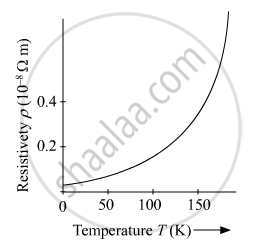
Plot a graph showing the variation of resistivity of a conductor with temperature.
उत्तर
The resistivity of a metallic conductor is given by
\[\rho = \rho_0 \left[ 1 + \alpha\left( T - T_0 \right) \right]\]
\\text { [where }\]
\[ \rho_0 = \text { Resistivity at reference temperature }\]
\[ T_0 =\text { Reference temperature }\]
\[ \alpha = \text { Coefficient of resistivity }\]
From the above relation, we can say that the graph between resistivity of a conductor with temperature is a straight line. But, at temperatures much lower than 273 K ( i.e. \[0 °C\], the graph deviates considerably from a straight line as shown below.
APPEARS IN
संबंधित प्रश्न
A metallic particle with no net charge is placed near a finite metal plate carrying a positive charge. The electric force on the particle will be
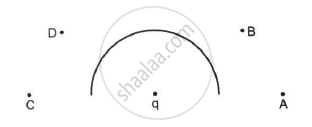
In the following figure shows a charge q placed at the centre of a hemisphere. A second charge Q is placed at one of the positions A, B, C and D. In which position(s) of this second charge, the flux of the electric field through the hemisphere remains unchanged?
(a) A
(b) B
(c) C
(d) D
The radius of a gold nucleus (Z = 79) is about 7.0 × 10-10 m. Assume that the positive charge is distributed uniformly throughout the nuclear volume. Find the strength of the electric field at (a) the surface of the nucleus and (b) at the middle point of a radius. Remembering that gold is a conductor, is it justified to assume that the positive charge is uniformly distributed over the entire volume of the nucleus and does not come to the outer surface?
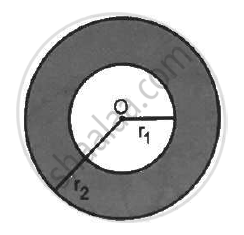
A charge Q is distributed uniformly within the material of a hollow sphere of inner and outer radii r1 and r2 (see the figure). Find the electric field at a point P at a distance x away from the centre for r1 < x < r. Draw a rough graph showing the electric field as a function of x for 0 < x < 2r2 (see the figure).
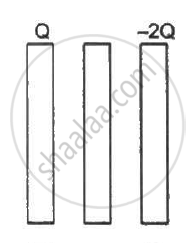
Three identical metal plates with large surface areas are kept parallel to each other as shown in the following figure. The leftmost plate is given a charge Q, the rightmost a charge −2Q and the middle one is kept neutral. Find the charge appearing on the outer surface of the rightmost plate.
Some equipotential surface is shown in the figure. What can you say about the magnitude and the direction of the electric field?
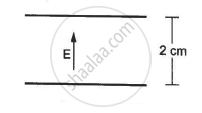
An electric field of magnitude 1000 NC−1 is produced between two parallel plates with a separation of 2.0 cm, as shown in the figure. (a) What is the potential difference between the plates? (b) With what minimum speed should an electron be projected from the lower place in the direction of the field, so that it may reach the upper plate? (c) Suppose the electron is projected from the lower place with the speed calculated in part (b). The direction of projection makes an angle of 60° with the field. Find the maximum height reached by the electron.
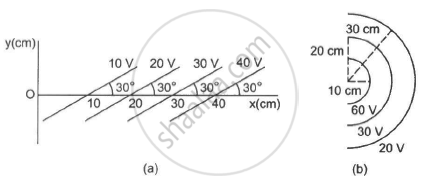
A uniform field of 2.0 NC−1 exists in space in the x-direction. (a) Taking the potential at the origin to be zero, write an expression for the potential at a general point (x, y, z). (b) At which point, the potential is 25 V? (c) If the potential at the origin is taken to be 100 V, what will be the expression for the potential at a general point? (d) What will be the potential at the origin if the potential at infinity is taken to be zero? Is it practical to choose the potential at infinity to be zero?
The force per unit charge is known as ______.
A charge Q is applied to a conducting sphere of radius R. At the sphere's centre, the electric potential and electric field are respectively
